Source : Final report on the S3 analysis
SOMMAIRE :
- Merci aux participants d'Einstein@Home
- Une brève vue d'ensemble du LIGO, de GEO et d'Einstein@Home
- Quel est le but d'Einstein@Home ?
- Que sont les pulsars, les étoiles à neutrons et les étoiles à quarks ?
- Comment Einstein@home recherche-t-il ces signaux ?
- Problème pratique : la puissance de calcul
- Qu'est-ce que la série de données LIGO S3
- Comment fonctionne la recherche Einstein@Home S3 ?
- Comment se présenterait un pulsar assez proche pour être détecté ?
- Cas type d'un résultat S3
- La sensibilité de la recherche n'est pas égale sur l'ensemble du ciel
- Pourquoi la recherche n'a t'elle pas la même sensibilité sur la totalité du ciel ?
- Résumé de l'analyse des résultats d'Einstein@Home S3
- Progrès depuis l'analyse de la S3 et perspectives pour les recherches futures ?
1. Merci aux participants d'Einstein@Home
Le travail scientifique exposé dans ce document n'aurait pas été possible sans les efforts et la généreuse contribution des dizaines de milliers de participants à Einstein@Home. Nous sommes très reconnaissants pour votre aide, et espérons que vous continuerez à participer au cours des prochaines années au projet Einstein@Home avec l'amélioration de la sensibilité des instruments LIGO et GEO. Ce document fournit une explication détaillée et un rapport sur l'état d'avancement des analyses que nous effectuons à l'aide de vos ordinateurs. Nous espérons que vous le trouverez intéressant.
Les résultats exposés ci-dessous ont été validés en interne et passés en revue par le groupe de chercheurs du "LIGO Scientific Collaboration" (LSC). Cependant, il est d'usage pour les scientifiques de soumettre leurs travaux à une réanalyse externe. Ainsi, en plus de ce rapport sur l'état d'avancement du projet, les résultats d'Einstein@Home, basés sur les futures phases de calcul scientifiques issues du LIGO et de GEO, seront soumis à des journaux scientifiques pour publication. Ces publications, qui paraîtront dans la littérature scientifique, rendront également hommage au travail des participants d'Einstein@Home.
La dernière section de ce document est la liste des auteurs de la S3 LIGO. Elle donne les noms et les affiliations institutionnelles des scientifiques et des ingénieurs qui ont conçu, mis en service, et manoeuvré les instruments du LIGO et de GEO ainsi que les systèmes d'analyse de données.
2. Une brève vue d'ensemble du LIGO, de GEO et d'Einstein@Home
Le projet Einstein@Home [1] se concentre sur la recherche d'ondes gravitationnelles émises par des étoiles ultra-denses tournant rapidement sur elles-mêmes, lesquelles sont appelées des pulsars. Les pulsars se forment lorsqu'une étoile "normale" s'effondre littéralement sous son propre poids. Ils possèdent la masse du soleil concentrée dans un rayon de seulement 10 kilomètres (une surface plus petite qu'une ville moyenne), correspondant à plus d'une dizaine de trillions de fois la densité d'un fil 2.1. Ils tournent extrêmement rapidement sur eux-mêmes, à une fréquence de plusieurs centaines de fois par seconde, jusqu'à 38 500 tours/min, c'est-à-dire plusieurs fois plus rapidement que le turbo d'une voiture de course. Le record est un pulsar [2] (PSR J1748-2446ad) qui effectue 43 000 rotations par minute sur lui-même.
Selon la théorie de la relativité générale d'Einstein [3, 4] , un pulsar n'est pas parfaitement rond, il agit comme un générateur d'ondes gravitationnelles, remuant et générant des ondulations dans la structure de l'espace-temps. Ces ondulations, nommées ondes gravitationnelles, s'éloignent de la source d'émission dans toutes les directions à la vitesse de la lumière, et peuvent éventuellement croiser le chemin de notre planète. Une poignée de projets de recherche internationaux tentent de détecter leur passage.

Figure 2.1 : vue d'artiste de l'ondulation de l'espace-temps appelée onde gravitationnelle. Ces ondulations se propagent à la vitesse de la lumière dans toutes les directions autour de la source d'émission. source : JPL [5]
Deux de ces projets, un aux Etats-Unis (LIGO), et une collaboration entre la Grande-Bretagne et l'Allemagne (GEO600), exploitent plusieurs détecteurs sous les auspices de la collaboration scientifique LIGO (LSC) [6, 7, 8, 9]. Les détecteurs sont conçus pour capturer les ondes gravitationnelles de l'une de ces quatre principales sources : le point d'équilibre orbital des couples de trous noirs où d'étoiles à neutrons, les explosions de supernova, un fond (stochastique) global, et les pulsars. Einstein@Home a été mis au point pour rechercher les ondes émises par ce dernier type de source : les pulsars. Bien évidemment, ces projets et Einstein@Home pourraient également découvrir quelque chose de nouveau et d'inattendu !
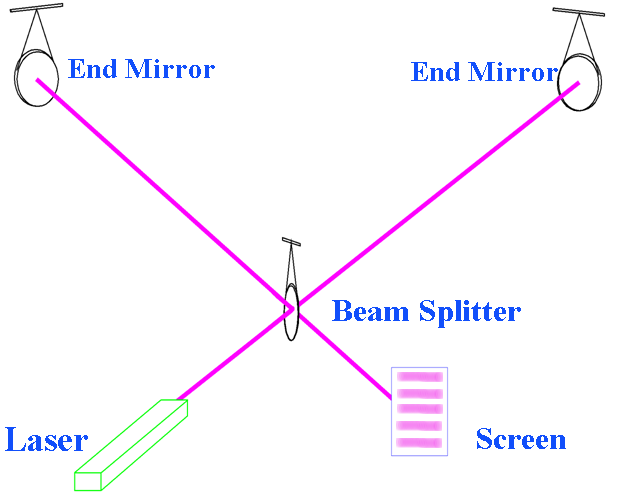
LIGO et GEO600 utilisent des détecteurs, connus sous le nom d'interféromètres, qui agissent comme d'énormes appareils d'observation. Plutôt que de corriger les distances le long de la surface de la Terre, comme le feraient les outils de mesure conventionnels, les interféromètres corrigent l'espace et le temps en utilisant la lumière du laser, qui voyage le long de leurs bras perpendiculaires d'un kilomètre de long. A l'intérieur de ces instruments un miroir semi-réfléchissant (Beam Splitter) dédouble le rayon laser en deux. Chacun de ces 2 faisceaux voyage dans l'un des bras de l'interféromètre, se reflète en arrivant devant le miroir situé à l'extrémité de chaque bras, puis revient vers miroir semi-réfléchissant. Lorsque les faisceaux se recombinent au niveau du miroir semi-réfléchissant, les champs électromagnétiques s'additionnent avec cohérence, ou se perturbent, en fonction des distances parcourues par les faisceaux dans leurs bras respectifs. En résulte une tâche lumineuse ou une tâche foncée à la sortie de l'interféromètre qui est un indicateur extrêmement précis de la moindre différence dans la longueur des bras. Si le polissage ou l'alignement des miroirs n'est pas parfait, alors les différents trajets des faisceaux correspondent à un échantillon distinctif de bandes foncées ou claires (appelées les «franges» ("fringes")) qui apparaîtra à la sortie de l'interféromètre, comme illustré dans 2.2. Les ondes gravitationnelles étireront et rétréciront alternativement et dans des proportions minuscules l'espace le long des bras de l'interféromètre, heurtant les miroirs suspendus durant leur course, et causant une oscillation de la fréquence durant le trajet aller-retour dans les bras de l'instrument. Ce qui enregistrera de minuscules oscillations correspondantes à la position des franges.
Figure 2.2 : la lumière du laser dans un interféromètre se dédouble pour suivre différents chemins le long des "bras". Les faisceaux reflétés sont recombinés par le miroir semi-réfléchissant (beam splitter) pour produire un échantillon des interférences montrées sur l'écran (screen). Le passage d'une onde gravitationnelle devrait entrainer des changements périodiques de ce diagramme d'interférence. Crédit : LIGO/LSC
Les interféromètres LIGO et GEO sont des instruments plus sophistiqués que le shéma présenté ci-dessus, avec des miroirs réfléchissants additionnels insérés dans la trajectoire des faisceaux pour amplifier la réponse du détecteur à une onde gravitationnelle. La position des miroirs est controlée par des systèmes réactifs pour «verrouiller» l'interféromètre, en maintenant une distance constante entre les miroirs avec une précision d'un nanomètre (10-9 mètres). Une perturbation suffisamment forte, telle qu'une tempête ou un tremblement de terre éloigné, peut mettre à mal le système réactif et entrainer un «déverrouillage» ; l'interféromètre n'est alors plus capable de mesurer l'effet des ondes gravitationnelles lorsque le système est déverrouillé. D'autres systèmes réactifs contrôlent l'alignement des miroirs, la qualité des lasers et des miroirs utilisés est si bonne que le faisceau dans sa totalité est regroupé dans une large frange simple, ou une simple tâche. Un détecteur photoélectrique surveille la tâche pour observer les oscillations de luminosité qui seraient provoquées par une onde gravitationnelle.
Entre 2002 et 2005, pendant la période liée à la mise en service des instruments, plusieurs séries de données, appelées la «science fonctionne» ("science runs"), ont été accomplies. Les résultats décrits dans ce rapport sont issus de la troisième série scientifique (S3). En ce moment (à l'heure de l'écriture de ce rapport, en septembre 2006) les instruments LIGO sont les plus sensibles des détecteurs terrestres d'ondes gravitationnelles, ainsi Einstein@Home se concentre sur l'analyse des données issues de LIGO.
En novembre 2005, LIGO a commencé sa cinquième série scientifique S5, qui est la première série avec une sensibilité de conception, il est prévu que cette phase dure jusqu'en août 2007. Cependant, le nombre de sources et leurs distances par rapport à Terre sont incertains, et durant les prochaines années de fonctionnement, il est tout à fait possible que les instruments LIGO et GEO puissent ne rien détecter. Mais ce ne sera pas la fin de l'Histoire ! Le travail de recherche et de développement consiste en une amélioration permanente des instruments pour la décennie suivante. Après la mise à niveau, les instruments atteindront un tel niveau de sensibilité que le fait de ne pas détecter d'ondes gravitationnelles issues d'une de ces sources serait si peu probable que ça serait de nature à remettre en cause la prévision d'Einstein sur l'existence des ondes gravitationnelles !
Les participants d'Einstein@Home à travers la planète font fonctionner un programme informatique qui a pour but de mettre en relief les faibles signaux gravitationnels par rapport à l'ensemble des bruits de fond, qui est la contrainte habituelle de ce type de mesures. Une partie de ce bruit de fond est provoqué par les vibrations des atomes à l'intérieur des miroirs et par les effets quantiques de la lumière. La mesure électronique de l'éclat de la lumière à la sortie de l'interféromètre peut également être joué par un haut-parleur ; le bruit aléatoire crée un « grondement et un sifflement » indéfinissables, c'est cette ondulation de l'espace-temps qui doit être extraite. Ce dossier (au format .au, 126ko) joue un échantillon des données issues du détecteur LIGO [10]. Un son similaire issu du détecteur GEO600 peut également être écouté en suivant ce lien (format .mp3, 187ko) [11]. Einstein@Home compare un modèle d'une onde gravitationnelle d'un pulsar qui devrait produire un segment de dix heures dans les données de l'interféromètre. Les événements à forte corrélation entre le modèle prévu et les données représentant les candidats à une onde gravitationnelle sont alors soumis à un examen minutieux. La puissance de calcul nécessaire pour identifier les pulsars candidats est énorme, elle exige des milliards de calculs qui doivent être exécutés pour un grand nombre de positions distinctes dans le ciel. La capacité pour mener à bien cette recherche sur des mois de données surpasse de loin les ressources informatiques considérables du LSC. Einstein@Home fonctionne comme un ordinateur mondial géant et est à même de fournir cette capacité. A la fin de l'été 2005, les participants d'Einstein@Home ont fini d'analyser les données de la série scientifique S3 (qui a eu lieu entre novembre 2003 et janvier 2004). Le nombre total d'opérations en virgule flottante (c'est-à-dire les additions, soustractions, multiplications et divisions) effectuées par Einstein@Home dans cette recherche S3 a été d'environ 1020 (un 1 suivi de 20 zéros). Depuis lors, Einstein@Home a effectué d'autres recherches en utilisant les données de la série scientifique S4. Une nouvelle recherche pour analyser les données S5 a commencé en juin 2006 et continuera jusqu'en 2007.
LIGO et GEO apprécient grandement l'aide des dizaines de milliers de participants à Einstein@Home qui font maintenant fonctionner le logiciel. Notre espoir est d'étendre le programme à une communauté beaucoup plus large au cours des prochaines années.
Pour aller au-delà de cette brève vue d'ensemble, lire svp le reste des pages fournies ici. Celles-ci fournissent une description plus détaillée d'Einstein@Home, le programme d'analyse de pulsar, et une partie de ce que nous avons appris jusqu'ici. Et continuez svp à utiliser Einstein@Home !
3. Quel est le but d'Einstein@Home ?
Einstein@Home est une méthode pour rechercher les ondes gravitationnelles émises par les étoiles très denses et en rotation rapide, tel que les étoiles à neutrons ou à quarks [12,13,14] . La fréquence des ondes est en général égale à deux fois la fréquence de la rotation de l'étoile, bien que d'autres fréquences soient également possibles. Ainsi, si une étoile tourne autour de son axe 100 fois par seconde, nous pourrions prévoir que des ondes gravitationnelles sont émises à une fréquence de 200 cycles par seconde (hertz).
Comme indiqué dans la vue d'ensemble, et pour différentes raisons qui sont expliquées dans le prochain chapitre, nous nous référerons aux sources ciblées par Einstein@Home c'est à dire aux ondes gravitationnelles émises par les pulsars, ou juste les pulsars pour faire court, bien que les sources qu'il serait possible de détecter soient beaucoup plus variées. Des exemples de sources possibles sont montrés dans la figure ci-dessous. Naturellement, Einstein@Home pourrait également découvrir quelque chose de complètement inattendu !
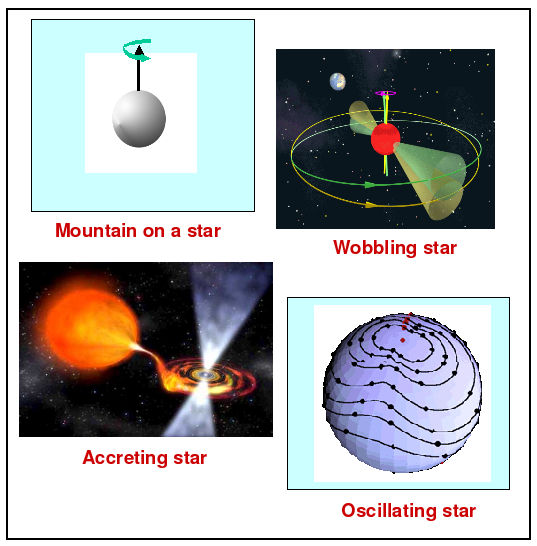
Figure 3.1 : Une source possibles d'onde gravitationnelle qui pourrait être trouvée grâce à Einstein@Home. Pour que l'onde soit discernable l'étoile schématisée dans la figure ci-dessus doit être une étoile à neutrons ou à quarks, ou quelque chose de nouveau qui dépasse les théories actuelles. Crédits : Mountain on a star (montagne sur une étoile), image par Jolien Creighton [15] ; Wobbling star (étoile tremblante), image par M. Kramer [16]; Accreting star (étoile en accrétion), image par Dana Berry/NASA [17] ; Oscillating star (étoile oscillante), image d'une simulation par Chad Hanna et Benjamin Owen.[18]
4. Que sont les pulsars, les étoiles à neutrons et les étoiles à quarks ?
Les pulsars ont pour le première fois été découvert en 1967 par Anthony Hewish and Jocelyn Bell [19, 20, 21, 22] grâce au radio-téléscope ci-dessous :

Figure 4.1: Le télescope de scintillation interplanétaire de Cambridge («rangée 4 acres»). Le télescope a été conçu et construit par Hewish et Bell pour mesurer les tailles angulaires des sources radio éloignées, en fonction du nombre de fois où elles scintillent lorsqu'elles brillent sous le vent solaire. Les pulsars ont été découverts par hasard pendant ce travail. (Photo: Graham Woan)
Les pulsars sont des étoiles très petites, très denses, et à rotation rapide qui se forment lorsque la pression au centre de ces énormes étoiles massives est si forte qu'elles ne peuvent plus résister à la pression et s'effondrent sur elles-mêmes. Dans ce processus, les couches externes de l'étoile sont arrachées à la pression dans une explosion supernova. Les restes d'une supernova qui s'est produite en 1054 après JC, est appelée la nébuleuse du crabe, vous pouvez la voire ci-dessous. Suite à la découverte du premier pulsar, un pulsar a également été trouvé dans la nébuleuse du crabe et a été baptisé du nom de celle-ci.

Figure 4.2: Nébuleuse et pulsar du crabe : N.A.Sharp/NOAO/AURA/NSF [23] . Cette série d'images montre la luminosité du pulsar toutes les millisecondes sur une rotation complète s'effectuant en 33.367 millisecondes.
Les pulsars ont une masse comparable à notre soleil, mais leur rayon n'est que d'environ 10km (la taille d'une ville). Une cuillère à café de matière pèse un milliard de tonnes.
Une étoile aussi dense s'appelle une étoile à neutrons car à une telle densité (comparable à la densité du noyau d'un atome), la matière se réduit quasiment à des neutrons. Le noyau des étoiles à neutrons est encore plus dense que le noyau d'un atome, et peut également contenir des hypérons, qui ressemblent à des neutrons et des protons mais en plus lourd. A une densité encore plus élevée la matière se dissout dans un mélange de quarks «hauts», «bas» et «étranges» [24], qui sont les constituants des neutrons, des protons, et des hypérons. Si la densité est assez élevé à proximité du centre, certaines de ces étoiles peuvent abriter des noyaux de quarks (et alors s'appeler une étoile hybride). Elles peuvent également s'appeler "étoiles étranges" ou "étoiles à quarks" entièrement constituées de quarks "hauts", "bas" ou "étranges" (à parts égales), bien que nous n'en connaissions pas assez sur les propriétés des quarks pour être sûrs que de tels objets exotiques existent ! La majeure partie du temps nous emploierons juste le terme « étoiles à neutrons » pour être concis, mais gardez à l'esprit que des objets plus exotiques sont également possibles.
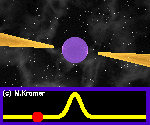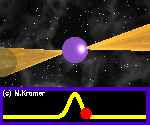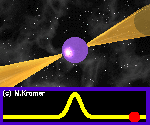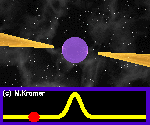
Nous observons les étoiles à neutrons et les pulsars car ces étoiles ont des champs magnétiques intenses et émettent des faisceaux de rayonnement électromagnétique à partir de leurs 2 pôles magnétiques. Le balayage du faisceau à travers l'espace lorsque l'étoile tourne, forme une sorte de phare cosmique. Imaginez le faisceau d'un phare balayant au-dessus de vous avec chaque rotation de la lumière du phare. Vous verriez une impulsion lumineuse pour chaque rotation. De même, si le faisceau du rayonnement électromagnétique d'une étoile à neutrons balaye la Terre, nous observons une impulsion radio à chaque fois que l'étoile tourne. Ainsi, les objets observés de cette façon s'appellent des pulsars. Une animation est montrée ci-dessous. Notez que parfois les impulsions radio sont dispersées et éparpillées par le gaz et la poussière interstellaires, ainsi elles peuvent apparaître et disparaître de manière imprévisible. Voir la section 3.2.1 de [25] pour plus de détails.
Figure 4.3: Une illustration animée du faisceau électromagnétique émis par un pulsar, par Michael Kramer.
Depuis la première découverte faite par Hewish et Bell, plusieurs milliers de pulsars ont été détectés de façon électromagnétique à l'aide de télescopes radio au sol. Ces pulsars ont des vitesses de rotation allant d'une fois toutes les quelques secondes à plusieurs centaines de rotations par seconde. La vitesse de rotation la plus rapide observée est de 716 fois par seconde (pour le pulsar PSR J1748-2446ad) ! Il est possible que notre Galaxie abrite une centaine de milliers d'étoiles à neutrons à rotation rapide, la plupart n'ont (jusqu'ici) pas encore été détectées. Cela est dû au fait que le faisceau du pulsar rate la Terre, les impulsions radio sont déviées par les nuages et poussières cosmiques, ou les étoiles à neutrons n'ont pas un champ magnétique assez intense pour produire un faisceau.
Einstein@Home est l'une des techniques les plus puissantes actuellement disponible pour rechercher les ondes gravitationnelles des étoiles à rotation rapide non encore détectées. Comme les ondes gravitationnelles ne sont pas émises sous la forme d'un faisceau (elles sont émises dans toutes les directions, bien que non-uniformément) et n'arrivent pas par impulsions, parce qu'elles ne pourraient être associées à aucune impulsion radio discernable, on pourrait inventer de nouveaux noms pour de telles sources. Par exemple on pourrait les appeler «pulsars à ondes gravitationnelles», «GWEN » ( Gravitational-Wave Emitting Neutron Stars - Etoiles à Neutrons Emettant des Ondes Gravitationnelles), ou des « gravitars ». Mais dans ce document, pour être le plus concis possible, nous emploierons le terme «pulsars» pour de telles sources.
La détection des ondes gravitationnelles émises par les pulsars fournirait de nouveaux moyens de découvrir et de localiser les étoiles à neutrons, et pourrait par la suite fournir un aperçu unique de la nature de la matière à ces densités.
Veuillez voir les références [12, 13,25,14] pour plus d'information sur les pulsars, les étoiles à neutrons et les étoiles à quarks.
5. Quelles sont les formes d'ondes gravitionnelles émises par les pulsars qui peuvent être détectées depuis la Terre ?
Si les ondes gravitationnelles erraient dans le vide, éloignées de tous corps massifs tels que le Soleil, Jupiter, ou la Terre, la détection des ondes gravitationnelles émises par les pulsars serait extrêmement simple. Tel que vu par le détecteur, le signal des ondes gravitationnelles d'une telle source aurait, pour une fréquence donnée, une tonalité sinusoïdale parfaite 5.1. Le signal pourrait être détecté en employant une méthode simple, connue sous le nom de transformée de Fourier [26]. Il existe une mise en oeuvre informatique très efficace pour cette méthode, connue sous le nom de transformée de Fourier rapide, qui rendrait la recherche du signal d'un pulsar en un problème facilement résolvable à l'aide d'un groupe de petits ordinateurs [27].
Cependant, un grand nombre de complications sont présentes car les détecteurs d'ondes gravitationnelles (LIGO [6] et GEO [7]) sont sur Terre. Le mouvement de la Terre, qui tourne autour de son axe et autour du soleil, modifie les ondes gravitationnelles mesurées par le détecteur. En d'autres termes, les mouvements de l'étoile et du détecteur modulent la forme des ondes. Cette modulation est comparable à la façon dont un émetteur radio FM code l'information en un signal radiofréquence.
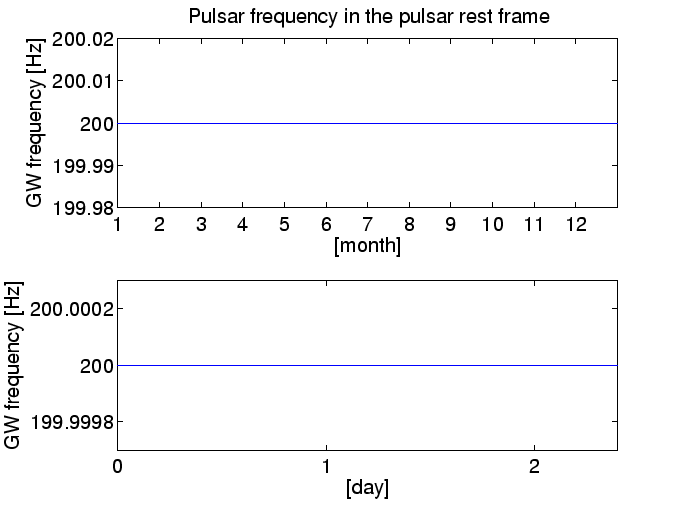
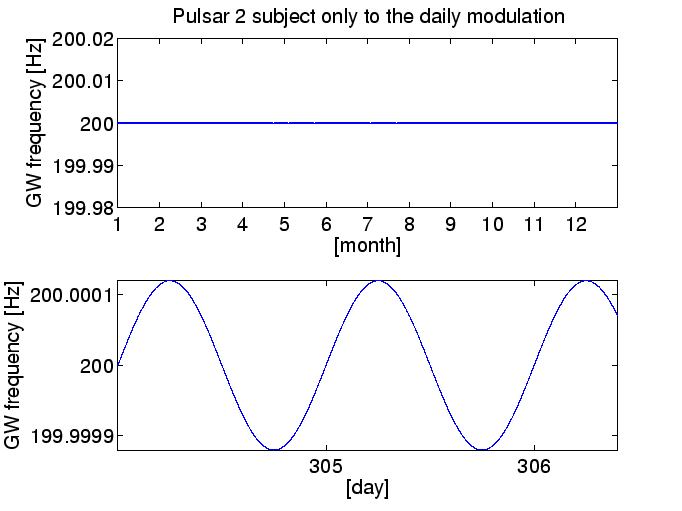
Voici quelques graphiques pour vous expliquer ce mécanisme. La figure 5.1 montre la fréquence d'une onde gravitationnelle d'un pulsar fictif dont la fréquence intrinsèque de rotation est de 100 cycles par seconde (100 hertz). La fréquence de l'onde gravitationnelle reçue par un hypothétique détecteur situé dans l'espace et suffisamment éloigné de notre système solaire est de 200 hertz suivant les indications de la figure. Même avec une durée supérieure à un an, cette fréquence ne change pas sensiblement : elle reste à 200 hertz 5.2.
Figure 5.1: La fréquence des ondes gavitationnelles reçue par un détecteur hypothétique situé dans l'espace et suffisamment éloigné de notre système solaire ou de tout autre corps massif est de 200 hertz. [En haut] (Aucune) modulation annuelle de la fréquence du signal (des ondes gravitationnelles). [En bas] (aucune) modulation journalière de la fréquence du signal pour les deux premiers jours de l'année.
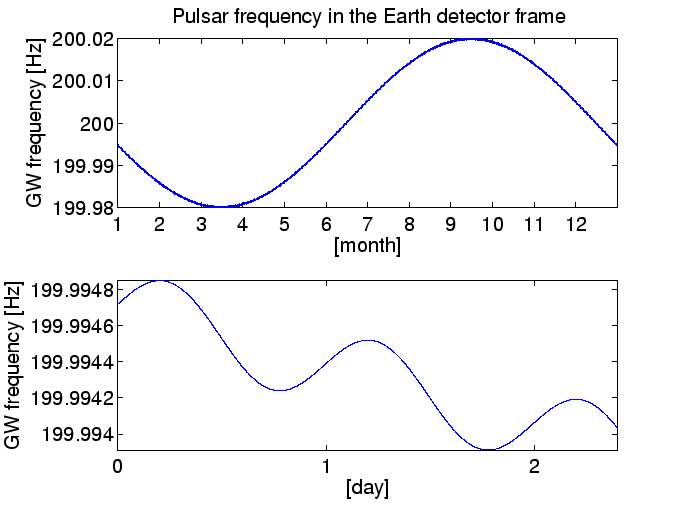
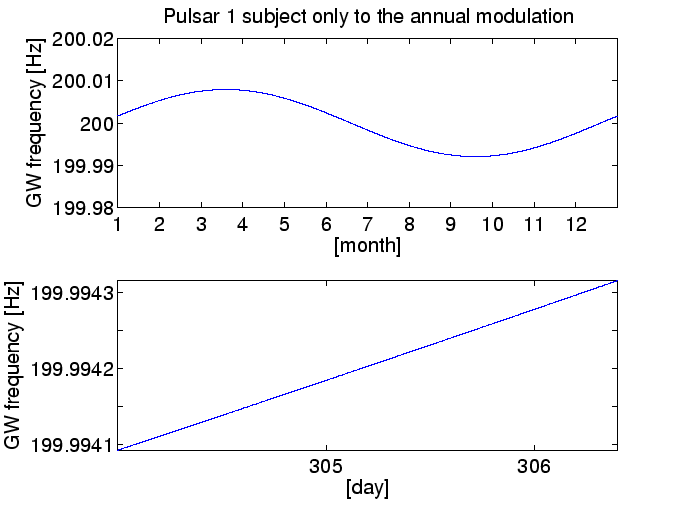
La figure 5.2 illustre la fréquence du même pulsar vu par un détecteur situé sur Terre. Notez qu'il y a une lente dérivation de fréquence sur une période de 12 mois, provoquée par le mouvement de la terre autour du soleil. A celà se superpose un rapide décalage de la fréquence, se déplaçant de haut en bas une fois toutes les 24 heures car la Terre tourne autour de son axe. Cette rapide dérivation de fréquence (une fois par jour) illustrée par le deuxième graphique est à peine évidente sur le premier graphique, car son amplitude est très petite.
Figure 5.2: La fréquence reçue par un détecteur situé sur Terre. [En haut] Modulation annuelle de la fréquence du signal sur un an. La modulation dans son ensemble est due au mouvement orbital de la Terre. La modulation due à la rotation de la Terre est à peine visible. [En bas] modulation journalière de la fréquence du signal pour les deux premiers jours de l'année. La modulation due à la rotation de la terre est maintenant nettement apparente.
Ces décalages de fréquence sont dus à l'effet Doppler [28]. C'est le même effet qui fait que le sifflement d'un train semble changer lorsque ce train passe devant un spectateur fixe. Quand le mouvement de la Terre rapproche le détecteur du pulsar, la fréquence du signal au niveau du détecteur est décalée vers une plus grande valeur (cet effet est également connu sous le nom de décalage vers le bleu (ou blueshift) de la fréquence). Plus tard, quand le mouvement de la Terre éloigne le détecteur du pulsar, la fréquence est décalée avec des valeurs plus faibles (déplacement vers le rouge (ou red-shift) de la fréquence).
Ces variations de fréquence sont petites mais ont des conséquences importantes. L'importance du décalage de fréquence éloigne de la fréquence nominale![]() .
.
![]() où
où ![]() est la rapidité de détection le long de la direction pointée vers la source et c est la vitesse de la lumière (c
est la rapidité de détection le long de la direction pointée vers la source et c est la vitesse de la lumière (c ![]() 300000 km/sec)
300000 km/sec)
La rapidité des détecteurs LIGO et GEO en raison du mouvement de rotation de la Terre est ![]() et la partie due à la rotation autour du soleil est
et la partie due à la rotation autour du soleil est ![]() . Par conséquent la modulation de fréquence introduite par l'orbite de la Terre autour du soleil est tout au plus d'environ une pour 10 000. C'est cent fois plus que la modulation de fréquence introduite par le mouvement de rotation de la Terre.
. Par conséquent la modulation de fréquence introduite par l'orbite de la Terre autour du soleil est tout au plus d'environ une pour 10 000. C'est cent fois plus que la modulation de fréquence introduite par le mouvement de rotation de la Terre.
La rapidité du détecteur pointant en direction d'une source n'est pas la même en fonction de l'emplacement des différentes sources, le modèle de modulation de fréquence qui serait observé dans le rendement du détecteur dépend de l'endroit exact de la source dans le ciel. La recherche de pulsars est un véritable challenge car chaque endroit du ciel a un modèle différent et nous devons rechercher dans les données tous les différents modèles.
6. Comment Einstein@home recherche t-il ces signaux ?
Nos détecteurs d'ondes gravitationnelles sont des instruments d'une sensibilité remarquable. En effet, ce sont les détecteurs les plus sensibles jamais construits, ils intégrent la technologie "cutting-edge" . Mais leur résultat est encore dominé par le "bruit" résultant de nombreuses sources différentes. Notamment, les mouvements du sol, les vibrations thermiques des atomes composant le systeme optique et les suspensions du détecteur, et les particules telles que le comportement quantique de la lumière du laser. (Ce dernier type de bruit est communément appelé bruit de grenaille (oushot noise) ). Le problème de l'analyse des ondes gravitationnelles a été décrit comme "essayer d'entendre une simple flûte au milieu d'un concert d'heavy metal" car nous devons identifier une forme d'onde "connue" cachée dans le bruit du détecteur.
La méthode standard employée pour rechercher des signaux dans le bruit est connue sous le nom de filtrage adapté ( matched filtering) ou filtrage optimal (optimal filtering) [29]. On peut prouver mathématiquement que le filtrage adapté est une technique linéaire optimale pour rechercher un signal connu inclus dans un bruit additif. L'idée est simple. Si nous connaissons la forme exacte de l'onde du signal, nous multiplions le rendement du détecteur pour cette forme d'onde, et le temps fini T. moyen. L'intégrale en résultant a deux limites. Une limite est donnée par le développement de la racine carrée du temps T, résultant du bruit aléatoire de l'instrument. (Ce processus est connu sous le nom de marche aléatoire ( ou random walk) 6.1 [30,31] ) L'autre limite se développe proportionnellement au temps T, elle est due au signal du pulsar. Ainsi si nous possédons assez de données, et assez de puissance de calcul, et connaissons la position exacte dans le ciel et la fréquence du pulsar, nous pourrions toujours choisir un T assez grand pour que la limite due à la source domine la limite due au bruit de l'instrument. Naturellement, T est limité à la durée pendant laquelle nous rassemblons réellement les données, ainsi le signal du pulsar doit avoir une certaine force minimum pour être discernable dans un temps fini.
En résumé, le filtrage adapté nous permet de trouver un signal extrêmement faible caché derrière le bruit, à condition que (1) nous ayons une série de données assez longue (2) que nous connaissions la forme exacte de l'onde du signal que nous recherchons. Cependant, Einstein@Home recherche des signaux émis par des sources inconnues, et donc la forme de l'onde exacte n'est pas connue : sa forme dépend de sa localisation dans le ciel (comme expliqué dans la section précédente) et de l'évolution intrinsèque de la fréquence de la source. Par conséquent, une recherche de sources inconnues nécessite de tester un filtrage adapté pour un nombre élevé de différentes formes d'onde, couvrant la gamme complète des localisations possibles dans le ciel et des évolutions intrinsèques de la fréquence. C'est la raison pour laquelle de telles recherches de paramètres adaptés sont extrêmement gourmandes en puissance de calcul informatique.
7. Problème pratique : la puissance de calcul
Comme décrit dans la section précédente, nous analysons les données en admettant qu'il y a un pulsar avec une fréquence donnée dans un point particulier du ciel, et en recherchant le signal correspondant à cette série de données. Dans la pratique nous établissons une grille très fine du ciel pour une fréquence et une vitesse de variation de la fréquence (ou dérivation de fréquence), et nous menons cette recherche pour chaque point de la grille.
La puissance de calcul exigée pour cette recherche se développe très rapidement en fonction de la durée du temps d'intégration T, principalement parce que la grille du ciel utilisée, ainsi que la fréquence et la dérivation de fréquence, deviennent plus précises à mesure que T augmente. Pour une recherche sur une bande de fréquence fixe, le temps de calcul est égal à T à la puissance 6 ! Ainsi l'augmentation du temps d'intégration T de 10 à 20 heures entraine une augmentation de la puissance informatique requise par un facteur 64 !
Concrètement, comme nous sommes limités pour les ordinateurs et grappes d'ordinateurs contrôlés par la collaboration scientifique LIGO (LSC) [8] nous ne pouvons pas rechercher pour des périodes T très longues. Ceci signifie que nous pouvons passer à coté de signaux discernables, plus T est grand, et plus nous pouvons fouiller derrière le bruit des instruments pour trouver un signal émis par un pulsar caché dans ce bruit.
C'est là que Einstein@Home et votre ordinateur peuvent nous aider. Avec beaucoup plus d'ordinateurs disponibles, nous pouvons fouiller en profondeur dans le bruit à la recherche de signaux. Le nombre d'ordinateurs directement disponibles au LSC est d'environ 1500, alors qu'Einstein@Home fournit actuellement environ 70 000 ordinateurs (en service). Quand vous faites fonctionner Einstein@Home sur votre ordinateur, vous obtenez des points pour votre travail, une fois que les résultats ont été validés. (Les résultats sont validés en les comparant aux résultats obtenus par d'autres utilisateurs pour le même travail.) les points que vous accumulez reflètent la quantité de travail valide que votre ordinateur (ou ordinateurs, si vous avez plusieurs) a accompli. En général, 100 points correspond au travail qui peut être effectué en 24 heures par un ordinateur faisant 1 milliard d'opérations en virgule flottante (ajouter, soustraire, multiplier ou diviser) par seconde.
8. Qu'est ce que la série de donnée LIGO S3
La construction des instruments LIGO et GEO a commencé au milieu des années 90. A la fin de la phase de construction, les instruments du LIGO ont été officiellement inaugurés les 11 et 12 novembre 1999. Depuis cette date, la commission des instruments a enchaîné plusieurs séquences d'ingénierie (E) et des étapes scientifiques (S) pour augmenter la sensibilité des instruments.
Voici les dates des cinq étapes scientifiques pour LIGO et GEO :
- S1: 23 Août - 9 Septembre 2002
- S2: 14 Février - 14 Avril 2003
- S3: 31 Octobre 2003 - 9 Janvier 2004
- S4: 22 Février - 23 Mars 2005
- S5: 4 Novembre, 2005 - (prévue jusqu'en Août 2007)
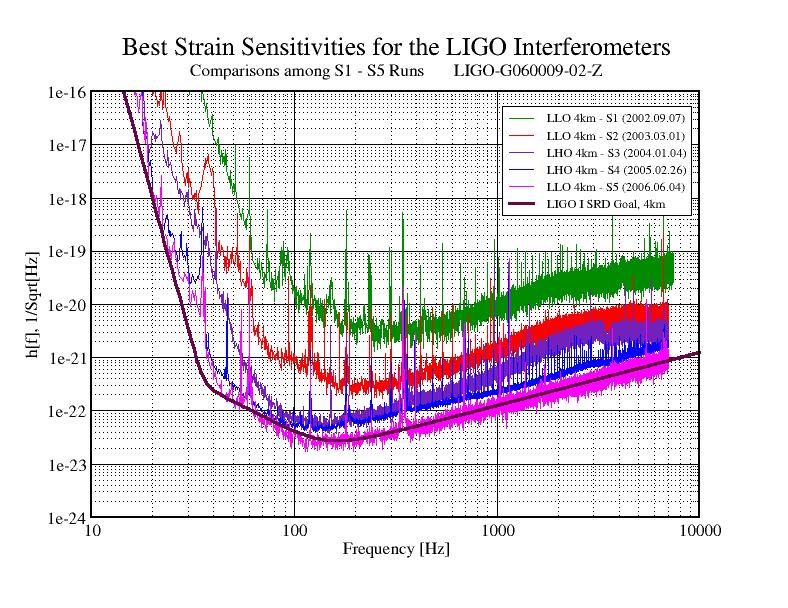
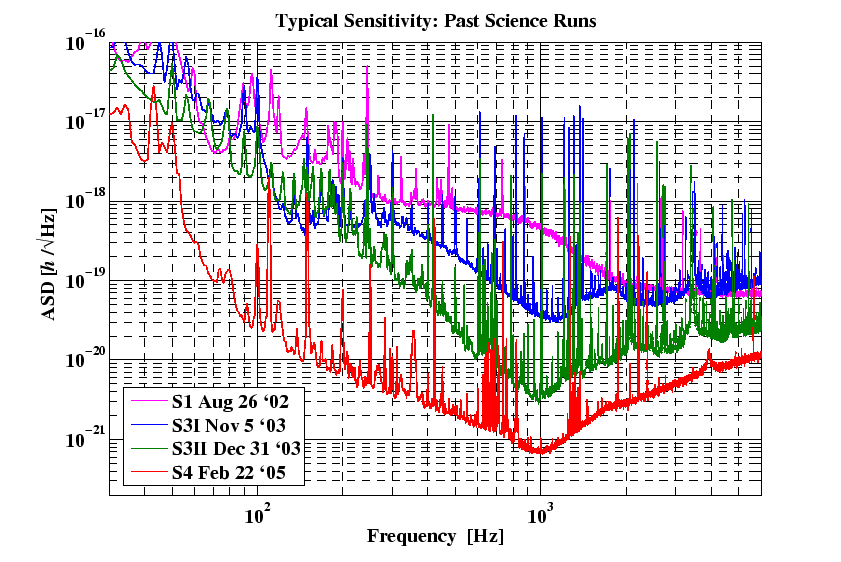
La sensibilité des instruments a considérablement augmenté à chacune de ces étapes, ces améliorations sont décrites dans la figure suivante. L'étape scientifique S5 actuelle devrait durer environ un an et demi, avec les détecteurs du LIGO fonctionnant essentiellement à la sensibilité de conception.
Figure 8.1: Les courbes montrent le niveau du bruit instrumental pour différentes fréquences pour les instruments LIGO de 4 km à Hanford et à Livingston, et comment il a diminué durant la mise en service des procédures. Le but fixé lors de la conception est la courbe noire SRD (Science Requirements Document) [32].
La figure suivante est un graphique similaire mais cette fois-ci pour GEO600. Suivant les indications de la figure, GEO600 était moins sensible que LIGO durant l'étape S3. Par conséquent, Einstein@Home utilisait seulement des données du LIGO pour l'analyse S3. Les résultats reportés dans les sections suivantes sont les résultats finaux de l'analyse Einstein@Home pour les données du LIGO S3.
Figure 8.2: Les courbes montrent le niveau du bruit instrumental pour GEO600. La longueur des bras de GEO600 est de 600m, ce qui est plus petit que la longueur de 4km des bras du LIGO. Généralement la sensibilité d'un observatoire d'ondes gravitationnelles par interféromètre laser augmente avec la longueur de bras. Mais le projet GEO600 étudie des techniques avancées alternatives pour obtenir une meilleure sensibilité. Celles-ci bénéficieront aux futurs projets de détection d'ondes gravitationnelles, y compris une mise à niveau prévue pour LIGO à la fin de cette décennie [7].
La fonction h(f) qui apparaît sur l'axe vertical de ces graphiques est une représentation spectrale de la "contrainte" h(t) mesurée par le détecteur pour différentes fréquences F. Pour apprécier la remarquable sensibilité de ces instruments, je vous renvoie au diagramme schématique d'un détecteur interférométrique d'ondes gravitationnelles. La contrainte h(t) est le changement partiel de la longueur apparente des bras qui serait provoqué par le passage d'une onde gravitationnelle au temps T. Ainsi une contrainte h=10-21 dans le LIGO avec des bras de 4Km correspond à un changement de la longueur de bras de 4 x 10-18 mètres. C'est environ mille fois plus petit que la taille d'un proton !
Certains des résultats de la collaboration scientifique LIGO obtenus à partir des données S1 et S2 sont rapportés dans [33,34,35,36] . Einstein@Home utilise des méthodes et un code similaire mais a commencé son travail d'analyse avec les données S3. Les ordinateurs d'Einstein@Home ont effectué les premières analyses des données LIGO S3 au début du mois d'août 2005, puis ont commencé les premières recherches sur les données S4. Le travail de post-traitement des données S3, basé sur les premiers résultats du S3, ont commencé quelques jours plus tard.
9. Comment fonctionne la recherche Einstein@Home S3 ?
La recherche Einstein@Home pour la série de données LIGO S3 utilise les 600 "meilleures" (c.-à-d. les plus sensibles) heures de données S3. L'instrument le plus sensible fonctionnant durant la S3 était le détecteur de 4 km de l'observatoire LIGO à Hanford, ainsi nous utilisons ces données. Celles-ci sont subdivisées en 60 segments totalisant dix heures de données chacun. Comme le fonctionnement des instruments ne se fait pas en continu, mais est souvent interrompu par le déverrouillage et d'autres événements, chacun de ces soixante segments de données de dix heures peuvent engendrer plus de dix heures en temps réel. Dans chacun des soixante cas, les 10 heures de données scientifiques ont été obtenues en moins de 13 heures temps réel.
Chaque segment de données est alors préparé comme suit. Les données sont calibrées en fonction du temps, en utilisant une méthode décrite dans [37]. Ceci produit un flux de données temporelles prélevées 16384 fois par seconde. Puis des morceaux de 30 minutes de données contiguës sont encadrés et subissent une transformée de Fourier, produisant des séries de données "transformée de Fourier courte" (SFT : "Short Fourier Transform"). Les lignes caractéristiques du dispositif9.1 sont supprimées. Le résultat final est une série de dossiers de 2901 SFT, qui couvrent une bande (superposée) d'environ 0.8 hertz. Chaque dossier contient 1200 transformées de Fourier (60 segments de dix heures x 20 SFT par segment de dix heures). La gamme de fréquence couverte va de 50.0Hz à 1500.5 hertz.
Un ordinateur qui fait tourner Einstein@Home (par exemple, VOTRE PC personnel) télécharge un de ces 2901 dossiers SFT. Chacun contenant 0.5 hertz de données utilisables, plus des "wings" de chaque côté.
De manière générale, l'ordinateur calcule le double d'une grille d'approximativement 30.000 points du ciel (une fois pour chacune des deux séries de données de dix heures) recherchant un pulsar à chacun de ces endroits, et effectue alors une étape de coïncidence conçue pour réduire le nombre des candidats "positifs faux" rapportés au serveur. Il fait ceci dans une bande de 0.1 hertz de largeur. Les candidats qui apparaissent dans les deux séries de dix heures sont rapportés au serveur d'Einstein@Home. Ces dossiers sont compressés avant qu'ils soient retournés, et ont une taille moyenne d'environ 110ko. Toutefois dans certains cas les dossiers sont beaucoup plus grands (quelques Mo) ou beaucoup plus petits, cela dépend des caractéristiques instrumentales qui apparaissent dans les données.
Une explication légèrement plus détaillée de la recherche est qu'à chaque point de la grille, et pour chaque fréquence dans une bande passante de 0.1 hertz, l'ordinateur calcule la "statistique F" [38], qui est le rendement d'un filtre optimal pour un pulsar sur un point dans la grille pour un des segments de dix heures de données. Si le bruit dans l'instrument est gaussien, alors la F-statistique suit une distribution x2 à quatre degrés de liberté [39] ; le paramètre de non-centralité est proportionnel au carré de l'amplitude de la source de l'onde gravitationnelle.
Les sources des candidats rassemblés par Einstein@Home sont celles pour lesquelles la valeur de la F-statistique satisfait 2F>25. Elles sont "groupées ensemble" dans l'espace des fréquences et écrites dans un dossier sur le disque de l'ordinateur. L'ordinateur répète alors ce procédé pour un segment de données de dix heures DIFFÉRENT. Chacune de ces deux étapes prend entre trois et douze heures sur un ordinateur moderne. Le temps exact dépend principalement de la vitesse du processeur et de la mémoire, et faiblement des données elles-mêmes. Puis, dans une troisième étape, les candidats trouvés dans chacun des deux segments de dix heures sont comparés, et seulement ceux qui coïncident à moins de 1 mégahertz pour la fréquence et 0.02 radian pour la position dans le ciel sont retenus. En moyenne, un ordinateur Einstein@Home a besoin de 11.1 heures de temps-processeur pour suivre ce processus en entier.
La liste des pulsars potentiels, qui sont apparus avec des paramètres cohérents dans les deux séries de données LIGO de dix heures, est retournée au serveur et stockée. Il y a 30 (paires de segments de dix heures) x (1500.5 hertz - 50.0 hertz) x (1 travail/0.1 hertz) = 435150 travaux d'analyse exécutés de cette façon.
Les résultats sont alors post-traités. L'idée fondamentale est simple. Si une source est présente quelque part dans le ciel et est assez forte pour être détectée avec confiance par l'instrument LIGO, alors elle devrait produire une grande valeur pour la F-statistique dans plusieurs des (ou tous les) 60 segments de données de dix heures. D'ailleurs, les données de localisation et la fréquence devraient respectivement être en accord avec respectivement une précision (déterminée par la simulation de Monte Carlo) de 0.02 radian et de 1 mégahertz.
Le post-traitement du code fonctionne par le chargement de la totalité des 60 résultats (chacun couvre 0.1 hertz d'un segment de données de dix heures) dans la mémoire puis pour trouver les "cellules" dans les paramètes spatiaux (position dans le ciel et fréquence) où un grand nombre de segments de données de dix heures contiennent une valeur de la F-statistique au-dessus du seuil 2F=25.
10. Comment se présenterait un pulsar assez proche pour être détecté ?
Si un pulsar est détecté avec certitude, nous nous attendons à ce qu'il dépasse le seuil de 2F=25 sur la plupart ou sur tous les 60 segments de données de dix heures. Ainsi cela mènerait à un nombre important de localisations dans les graphiques de coïncidence présentés dans les prochaines sections. En fait, nous verrons dans les sections suivantes que le bruit gaussien produit à lui seul un nombre d'environ six par hasard.
Comment pouvons-nous savoir que ceci fonctionnera vraiment ? Pour le vérifier, nous utilisons deux méthodes de vérification différents pour savoir si l'analyse des données fonctionne correctement et serait capable de détecter une source.
Injections matérielles
Lorsque les données S3 ont été recueillies, onze signaux simulés de pulsar « ont été injectés » en temps réel dans le matériel de détection. Pour être sûr qu'elles ne poseraient pas de problèmes imprévus dans l'analyse des données, ces injections matérielles n'étaient pas "en marche " durant la série S3. Ainsi elles ne reproduisent pas complètement ce qui se produirait si un vrai signal était présent. Ces faux signaux de pulsar sont présents dans environ un tiers (approximativement 20) des segments de données de dix heures analysés par Einstein@Home.
Injections logicielles
En préparant les données S3 (finales, une seconde fois) pour les distribuer sur Einstein@Home, nous avons ajouté une série de six pulsars simulés par logiciel. Les signaux étaient présents dans toutes les données, mais leurs amplitudes ont été choisies proches du seuil de sensibilité prévu. Par conséquent, ces signaux simulés excèdent le seuil de 2F=25 dans environ la moitié (approximativement 30) des segments de données de dix heures analysés par Einstein@Home.
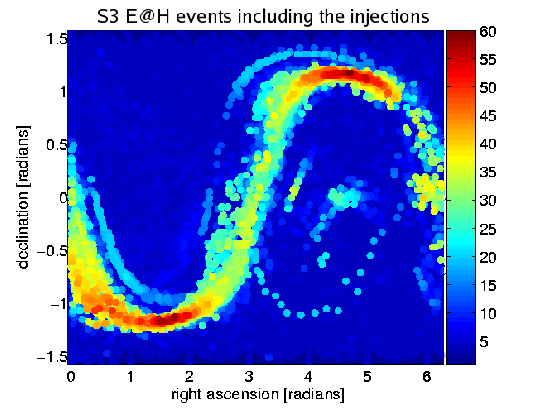
Les figures ci-dessous sont des cartes du ciel qui représentent les bandes de fréquence des signaux (matériels et logiciels) injectés artificiellement. Noter le grand nombre de segments pour lesquels F dépasse le seuil fixé.
Les deux figures suivantes montrent une partie des résultats des injections matérielles et logicielles. Ces pulsars (simulés) ont les paramètres 10.1 suivants :
| injection de pulsar matériel | 6.16125E-23 | 108.8571594 | -0.0806666107 | 0.444280306 | 5.5318207 | 3.11318871 | -0.583578803 | 20 |
| injection de pulsar logiciel | 1.56171E-23 | 574.1 | -0.9281 | -0.2218 | 4.0345 | 3.7569 | 0.0601 | 29-31 |
Ces figures sont des cartes colorisées de la sphère céleste. Les coordonnées sont les coordonnées astronomiques conventionnelles : ascension droite (right ascension) [40] et déclinaison (declination) [41]. Sur Terre, cela correspond en gros à la longitude et à la latitude. Les cartes en couleur montrent le nombre de segments de données de dix heures qui excèdent le seuil de 2F=25 dans chacune des régions du ciel et de fréquence. Dans la légende nous récapitulons ceci par « carte en couleur du nombre de coïncidences parmi les soixante segments de données de dix heures ». Un puissant signal de pulsar excéderait le seuil de 2F=25 dans beaucoup ou pour chacun des soixante segments de données, et virerait au rouge sur la carte. Les régions sans signaux de pulsar discernables excèdent le seuil par un simple accident aléatoire (la chance !) pour une poignée (environ six) de segments de données et tendent vers le bleu foncé sur la carte
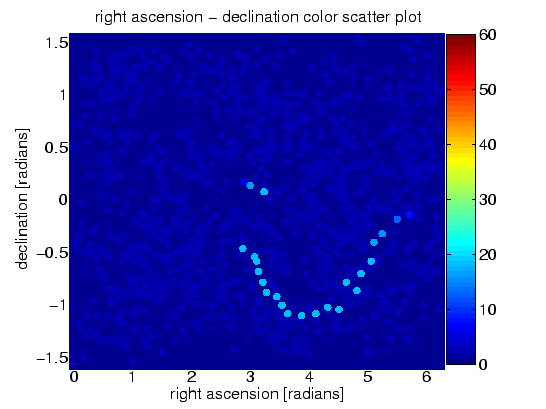
(b) déclination - carte de fréquence
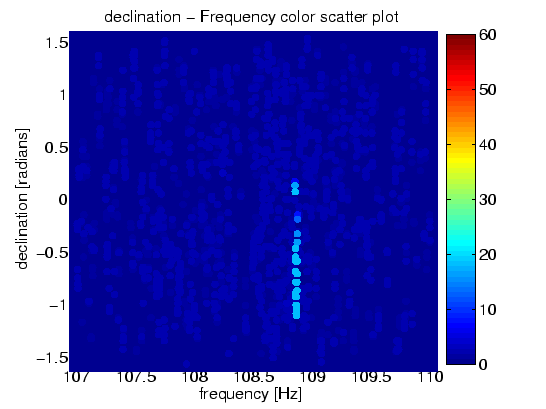
Figure 10.1 : Injection matérielle. Carte en couleur du nombre de coïncidences parmi les 60 soixante segments de données de dix heures. (a) carte du ciel. (b) plan de déclinaison des fréquences.
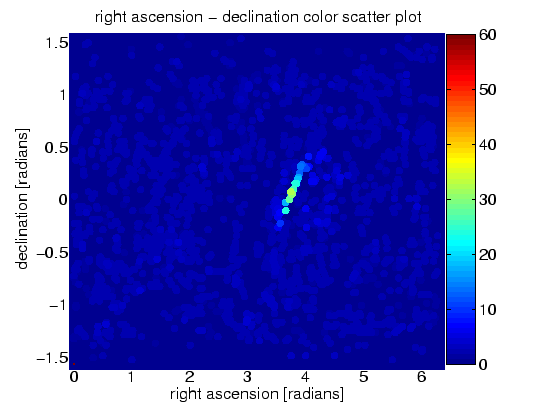
(b) déclination - carte de fréquence
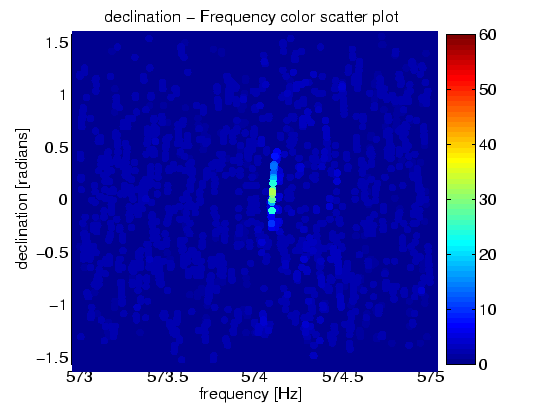
Figure 10.2 : Injection logicielle. Carte en couleur du nombre de coïncidences parmi les 60 soixante segments de données de dix heures. (a) carte du ciel. (b) plan de déclinaison des fréquences.
La valeur la plus importante dans le tableau ci-dessus est l'amplitude de la déformation liée à l'onde gravitationnelle ![]() . L'amplitude de cette déformation
. L'amplitude de cette déformation ![]() dépend de la distance au pulsar, la fréquence de l'onde gravitationnelle, l'ellipticité
dépend de la distance au pulsar, la fréquence de l'onde gravitationnelle, l'ellipticité ![]() de la source et du moment d'inertie de la source. (Elle est proportionnelle à l'ellipticité, au moment de l'inertie, et à la fréquence au carré, et inversement proportionnelle à la distance.)
de la source et du moment d'inertie de la source. (Elle est proportionnelle à l'ellipticité, au moment de l'inertie, et à la fréquence au carré, et inversement proportionnelle à la distance.)
La figure ci-dessous montre la relation entre ![]() et la distance (en parsec) pour une ellipticité fixe
et la distance (en parsec) pour une ellipticité fixe ![]() et pour les mêmes fréquences d'injection de pulsars (matérielles et logicielles) mentionnées ci-dessus. L'ellipticité est là pour mesurer à quel point une étoile est allongée et bosselée. Cette valeur de
et pour les mêmes fréquences d'injection de pulsars (matérielles et logicielles) mentionnées ci-dessus. L'ellipticité est là pour mesurer à quel point une étoile est allongée et bosselée. Cette valeur de ![]() est la limite supérieure des valeurs considérées comme raisonnables pour une étoile à neutrons normale, bien que certaines possibilités plus exotiques telles que les étoiles à quarks pourraient avoir des ellipticités 10 à 100 fois plus grandes [42] et ainsi produire des ondes gravitationnelles d'une amplitude 10 à 100 fois plus élevées
est la limite supérieure des valeurs considérées comme raisonnables pour une étoile à neutrons normale, bien que certaines possibilités plus exotiques telles que les étoiles à quarks pourraient avoir des ellipticités 10 à 100 fois plus grandes [42] et ainsi produire des ondes gravitationnelles d'une amplitude 10 à 100 fois plus élevées ![]() .
.
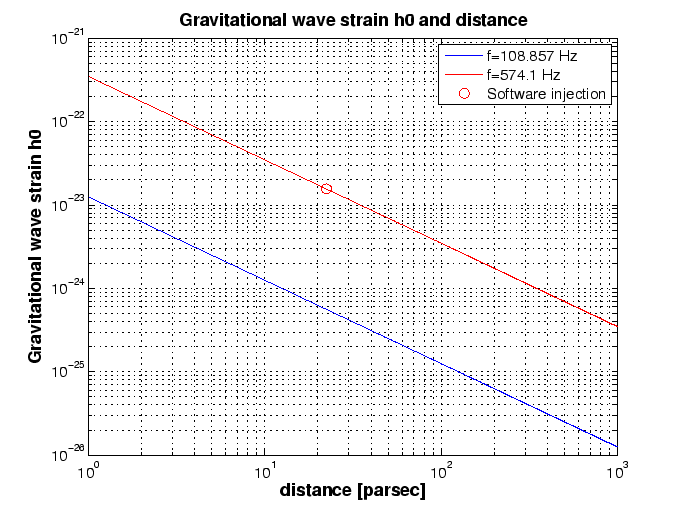
Figure 10.3 : L'amplitude de la déformation liée à l'onde gravitationnelle ![]() est fonction de la distance en parsecs. Ici l'ellipticité
est fonction de la distance en parsecs. Ici l'ellipticité ![]() du pulsar est présumée être
du pulsar est présumée être ![]() (et la valeur conventionnelle pour ce moment d'inertie est de
(et la valeur conventionnelle pour ce moment d'inertie est de ![]() . Le cercle rouge indique l'injection logicielle décrite ci-dessus. Un pulsar avec
. Le cercle rouge indique l'injection logicielle décrite ci-dessus. Un pulsar avec ![]() et les mêmes propriétés que le logiciel qui injecte de faux pulsars serait d'environ 25 parsecs. Le fait qu'Einstein@Home arrive à détecter ces pulsars injectés par un logiciel démontre qu'il y a une probabilité raisonnable de détecter des pulsars à une distance de quelques dizaines de parsecs. Ces courbes sont tirées de l'équation (25) de [38]
et les mêmes propriétés que le logiciel qui injecte de faux pulsars serait d'environ 25 parsecs. Le fait qu'Einstein@Home arrive à détecter ces pulsars injectés par un logiciel démontre qu'il y a une probabilité raisonnable de détecter des pulsars à une distance de quelques dizaines de parsecs. Ces courbes sont tirées de l'équation (25) de [38]
Vous pouvez voir qu'avec la série de donnée S3, nous devrions pouvoir détecter des pulsars jusqu'à une distance de quelques dizaines de parsecs (environ cent années-lumière). Cette distance dépend de la fréquence de la source. Nous prouverons également plus tard que cette distance dépend de la localisation de la source dans le ciel.
La figure ci-dessous montre un résultat sorti de l'étape de post-traitement. Il montre, dans une bande de fréquences comprises entre 300 à 325 hertz, et pour chaque point de la grille du ciel, le nombre maximum de segments de données de dix heures pour lesquels la valeur de 2F est supérieure à 25. Comme il y avait soixante segments de données de dix heures différents, ce nombre peut varier de 0 à 60.
La première figure, 11.1 (a), montre une carte en couleur de la déclinaison et de l'ascension droite qui totalise, pour chaque point de la grille, le nombre de coïncidences. La deuxième figure, 11.1 (b), montre une carte couleur de la déclinaison - et de la fréquence qui totalise, pour chaque point de la grille, le nombre de coïncidences. Ces deux figures montrent que dans cette partie du ciel nous n'avons aucun candidat dans la bande de fréquence 300-325 hertz. Cette bande est un cas type d'une bande "propres" dans nos données du détecteur LIGO S3 à Hanford. La majorité des bandes de fréquences sont aussi propres que cet exemple.
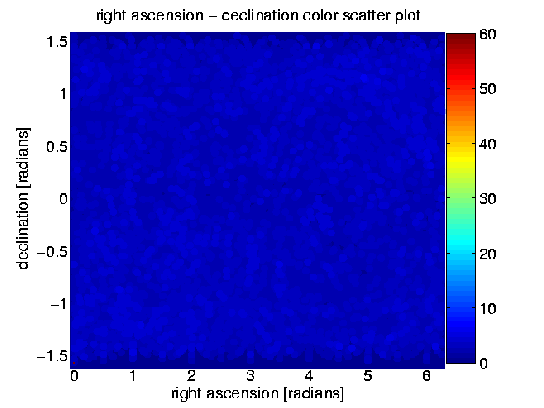
(b) carte de déclinaison et de fréquence
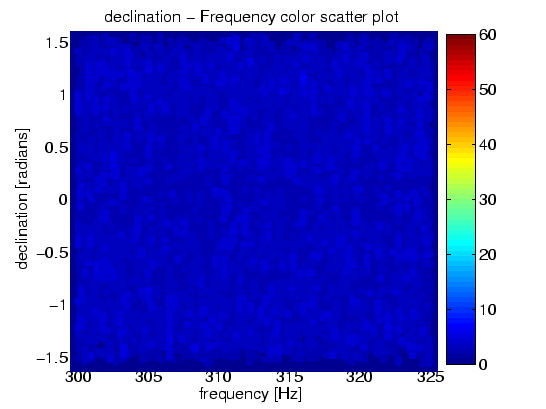
Figure 11.1: Carte couleur du nombre de coïncidences parmi les soixante segments de données de dix heures pour la gamme de fréquences allant de 300 à 325 hertz. (a) carte du ciel (b) carte de déclinaison et de fréquences
Les "bruits" instrumentaux les plus bénins ("bruits" gaussien) peuvent produire un nombre de coïncidences d'environ 6 par tirage aléatoire. Pour ce type de bruit, tout candidat ayant un nombre de coïcidences plus grand que, par exemple, 20 est un candidat potentiel pour des études plus approfondies.
Dans cette bande de fréquence (300 à 325 hertz) le plus grand nombre de segments qui ont contenu une signature de pulsar cohérente s'est avéré être égal à 6, conformément aux propriétés du bruit gaussien. Contrairement à ceci, un puissant signal de pulsar serait apparu sur tous, ou presque tous les, 60 segments. Une source proche de notre seuil fixé pour la détection serait apparue dans plusieurs (disons plus de la moitié) des segments. Ceci a été illustré dans la section injection matériel/logiciel pour quelques "fausses" sources ajoutées à la série de données.
En se basant sur ce graphique, nous concluons qu'Einstein@Home n'a trouvé aucun candidat ou perturbation crédible dans la bande de fréquence 300-325 hertz.
Les résultats complets de la série de données S3 d'Einstein@Home (de 50 à 1500 hertz) sont résumés dans la section 14.
12. la recherche n'a pas le même niveau de sensibilité sur la totalité du ciel
Comme cela a été décrit auparavant, le signal d'un pulsar est modulé par la rotation de la terre autour de son axe et de son mouvement autour du soleil. L'intensité et la nature de cette modulation dépend de la localisation du pulsar dans le ciel. Comme les résultats sortis du détecteur sont parsemés de bruits instrumentaux purement sinusoïdaux (par exemple, la résonance à 60 hertz et modes violons liés aux suspensions des câbles du miroir optique) ceci signifie que notre recherche est plus sensible pour certaines régions du ciel.
Les deux figures suivantes sont des graphiques similaires aux figures précédentes mais dans une bande de fréquences à proximité des modes violons liés aux suspensions optiques (340-350 hertz). Un nombre important des éléments optiques du LIGO sont suspendus à des câbles, et les fluctuations thermiques ou d'autres sources de bruit font vibrer ces câbles comme le pincement d'une corde de violon, d'où l'expression "modes violons". Les modes violons des suspensions optiques produisent de faux candidats. (Par exemple, comparez le nombre de coïncidences dans ces deux figures à celles des figures dans la section précédente pour la bande de fréquence 300-325 hertz.)
La carte du ciel (a) montre que les modes violons produisent "une ceinture bruyante" dans le ciel. Le long de cette ceinture, la ligne spectrale apparaît comme un signal de pulsar (voir la prochaine section pour connaître les raisons!). C'est essentiellement pour ça que nous n'avons pas beaucoup de sensibilité pour un signal dans cette région.
Le graphique fréquence-déclinaison montre que les modes violons rendent une région assez large du ciel peu sensible aux ondes gravitationnelles émises par un pulsar, bien que la région obscurcie couvre uniquement une gamme restreinte de fréquences et laisse toujours une bonne sensibilité sur une large partie de l'espace resté intact de tout bruit. En fait, en préparant les données (finales, une seconde fois) de la série S3 pour l'analyse par Einstein@Home, les modes violons ont été enlevés pour réduire le nombre de faux candidats
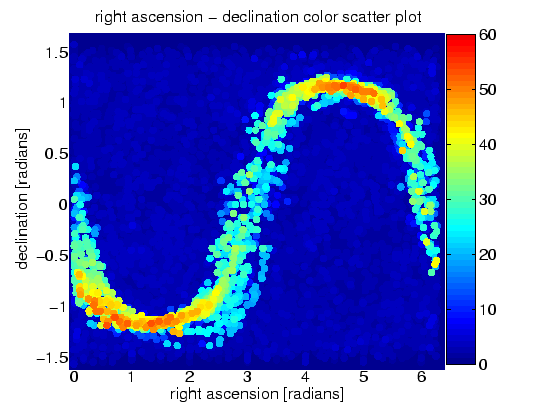
(b) carte de déclinaison et de fréquence
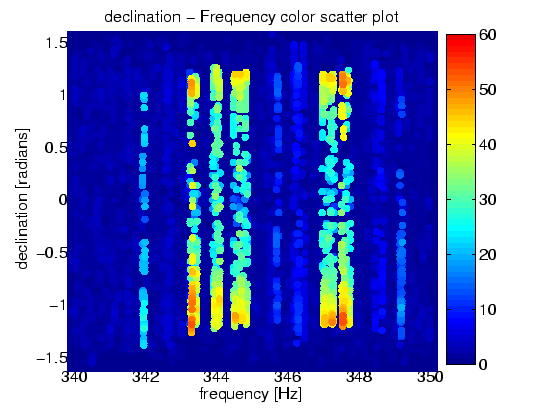
Figure 12.1: Carte en couleur du nombre de coïncidences parmi soixante segments de données de dix heures dans la gamme de fréquences 340-350 hertz. Les premières résonances en mode-violon (340-350 hertz) produisent des candidats importants. Comme ils ne sont pas produits par des pulsars, ces événements fallacieux s'appellent des "faux candidats" ou "fausses alarmes". (a) carte du ciel (b) carte de déclinaison et de fréquences.
Dans la prochaine section, nous allons expliquer pourquoi les sources de bruits instrumentaux sinusoïdales telles que les modes violons des suspensions des câbles du miroir optique produisent ces modèles caractéristiques (larges cercles) sur la sphère céleste.
13. Pourquoi le niveau de sensibilité de la recherche n'est-il pas le même sur la totalité du ciel ?
Il s'avère que la recherche de pulsar Einstein@Home est plus sensible pour certains secteurs du ciel. Cela est dû au fait que l'instrument utilisé implique quelques sources de bruits (lignes étroites de fréquences) qui miment les signaux qui seraient produits par des pulsars proches d'un grand cercle ovale dans la sphère céleste et ainsi obscursissent les vraies sources potentielles. (Le cercle a en son centre une ligne moyenne qui va de la Terre au Soleil durant l'enregistrement S3). Cet effet rend Einstein@Home moins sensible à proximité de ce grand cercle.
Pour comprendre les raisons pour lesquelles nous n'avons pas la même sensibilité sur l'ensemble du ciel, étudiez les signaux du détecteur qui seraient produits par quatre pulsars hypothétiques dans différents endroits du ciel pendant la série scientifique S3. (Note : la localisation dans le ciel devra être considérée comme un point sur la sphère céleste, comme réprésenté sur l'écran de veille Einstein@Home).
- Un pulsar situé juste au-dessus du Pôle Nord de la Terre (en rose)
- Un pulsar situé juste au-dessus du plan orbital de la Terre autour du soleil (en vert)
- Un pulsar situé en direction de la révolution de la Terre autour du Soleil pendant le S3 (en jaune)
- Un pulsar aligné avec la Terre et le Soleil durant l'enregistrement du S3 (en bleu-clair)
Les positions relatives au Soleil et à la Terre de ces quatre pulsars hypothétiques sont montrées dans les schémas suivants :
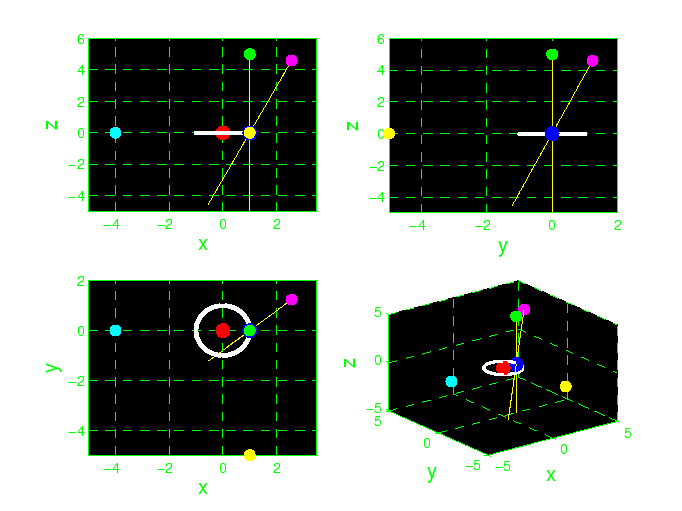
Figure 13.1: Diagramme schématique (pas d'échelle) décrivant les positions de quatre pulsars hypothétiques. Le diagramme en bas à droite est une vue d'ensemble tridimensionnelle du système solaire, montrant la Terre (en bleu) qui tourne autour du Soleil (en rouge). L'orbite de la Terre autour du Soleil est montrée en blanc. Les trois autres diagrammes sont des projections sur trois plans perpendiculaires. Le pulsar #1 (en rose) se situe juste au-dessus du Pôle Nord de la Terre et n'a donc aucune modulation journalière de fréquence. Le pulsar #2 (en vert) se situe juste au-dessus du plan d'orbite de la Terre autour du Soleil, et n'a donc aucune modulation annuelle de fréquence. Le pulsar #3 (en jaune) est dans la direction (dans le sens) de révolution de la Terre autour du Soleil durant l'enregistrement S3, et a donc un décalage vers le rouge maximum. Le pulsar #4 (bleu-clair) est situé sur la même droite Terre-Soleil durant l'enregistrement S3.
Les différentes ondes de pulsar vues par le détecteur dans chacun de ces quatre cas apparaissent comme suit :
- Aucune modulation journalière de fréquence, juste une modulation annuelle.
- Juste une modulation journalière de fréquence, aucune modulation annuelle.
- La vitesse de variation de la modulation annuelle de fréquence se réduit.
- La vitesse de variation de la modulation annuelle de fréquence augmente.
Notez que dans les cas [2] et [3], pendant des jours où des semaines le signal du pulsar ressemble fortement à un "bruit" instrumental lié au détecteur. Ainsi la ligne "pollue" une région du ciel, qui correspond à un grand cercle sur la sphère céleste, composée de ces directions perpendiculaires à la droite Terre-Soleil.
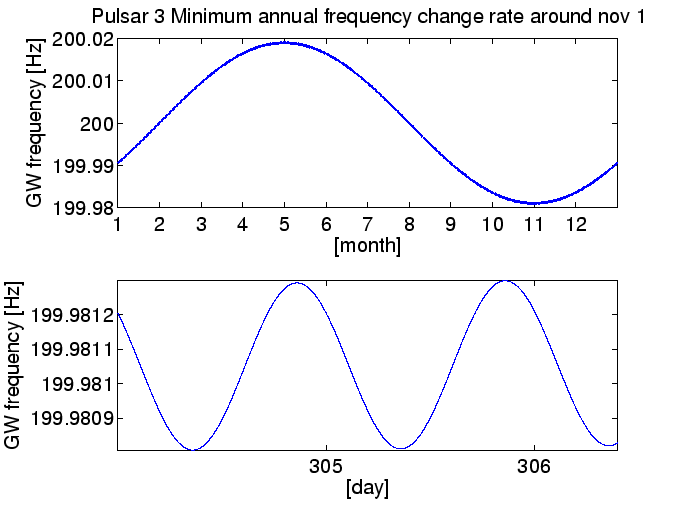
Figure 13.2: Un pulsar juste au-dessus du Pôle Nord de la Terre. (en haut) la modulation annuelle (en bas) la modulation journalière aux alentours du 1er novembre. Pour ce pulsar, il n'y a aucune modulation journalière liée à la rotation de la Terre.
Figure 13.3: Un pulsar juste au-dessus du plan orbital de la Terre autour du Soleil. En haut: La modulation annuelle est absente. En bas: La modulation journalière.
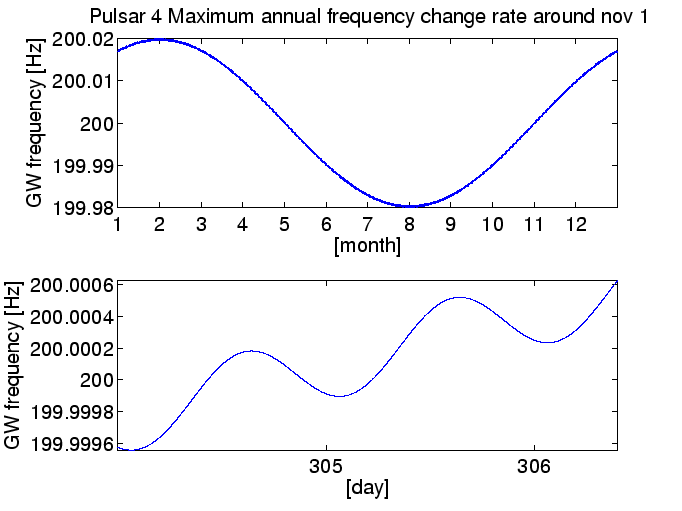
Figure 13.4: Un pulsar en direction de la vitesse moyenne de la Terre autour du Soleil durant l'enregistrement S3. En haut: La variation de la vitesse de la modulation annuelle se réduit tout au long de l'enregistrement de la S3. En Bas: La seule modulation significative pendant le S3 vient des variations journalières.
Figure 13.5: Un pulsar sur la même droite Soleil-Terre durant l'enregistrement S3. En haut : La vitesse de variation de la modulation annuelle augmente tout au long de l'enregistrement S3. En Bas: Les effets de la modulation annuelle sont significatifs sur une échelle exprimée en jours.
Il est maintenant facile de savoir pourquoi les artéfacts instrumentaux qui sont des fonctions sinusoïdales fonction du temps imitent des pulsars placés près d'un grand cercle particulier dans le ciel. N'importe quel pulsar situé dans le plan défini par les directions des pulsars #2 et #3 produit un signal sur le détecteur dans lequel la modulation annuelle de fréquence est absente ou très faible pendant la durée de l'enregistrement S3. Ce plan est perpendiculaire pendant l'enregistrement S3 à la droite allant de la Terre au Soleil. Ainsi, les artéfacts instrumentaux qui ont une fréquence fixe semblent se situer dans ce plan, et l'intersection de ce plan avec la sphère céleste est un grand cercle centré sur la droite Terre-Soleil.
14. Pourquoi et comment les données devront-elles être réanalysées ?
Après avoir analysé la série de données S3, nous avons apporté plusieurs améliorations :
- Les données ont été réajustées en utilisant une évaluation de la qualité des données finales (appelée la 5ème version de contrôle qualité des données - data-quality flags ) et le calibrage de l'instrument (appelé la 3ème version du calibrage de l'instrument).
- Les lignes parasites les plus connues ont été supprimées de l'ensemble des données pour empêcher de faux signaux.
- En complément de l'ajout de matériel, un logiciel d'ajout de pulsars a été ajouté. Pour une explication de cet ajout, voir la section ajout de matériel et de logiciel
- Des paires de segments ont été regroupées pour maximiser le nombre de segments de dix heures contenant les signaux injectés par le matériel.
La ré-analyse de la S3 a été accomplie par des participants d'Einstein@Home le 2 août 2005 (suivi par une longue période durant laquelle les résultats et les outils de l'analyse ont été passés en revue et contrôlés). Les deux graphiques suivants (Fig 14.1) résument les résultats de VOTRE analyse Einstein@Home des données LIGO S3
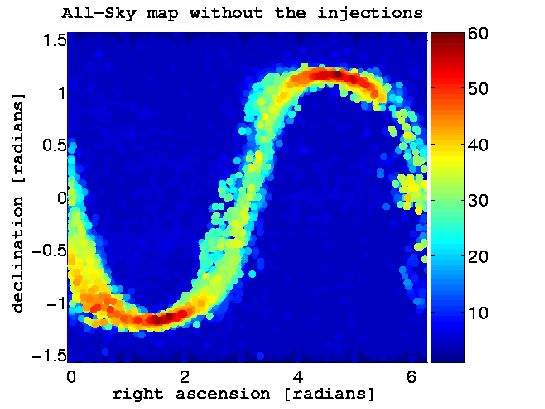
Figure 14.1 : Carte de la totalité du ciel couvert par les résultats de la S3 sur toutes les fréquences (50Hz à 1.5kHz) (a) en incluant l'ajout de matériel/logiciel, et (b) tous les ajouts sont coupés.
La Figure 14.1 (a) montre la carte de la totalité du ciel pour tous les candidats da la 3ème série scientifique du LIGO pour une bande de fréquence de recherche allant de 50 hertz à 1.5 kilohertz. Cette Figure inclu les fréquences auxquelles les signaux des pulsars simulés ont été injectés par le logiciel ou le matériel. La Figure 14.1 (b) montre la carte de la totalité du ciel en excluant les "faux signaux" (de l'ordre de 0.2 hertz) dans lesquels les pulsars simulés avaient été injectés dans le logiciel ou le matériel. Les lecteurs qui sont intéressés peuvent trouver les paramètres matériels et logiciels d'injections dans ce tableau. Les fréquences précises de ces signaux sont indiquées dans ce tableau (deuxième et troisième colonnes).
Nous voyons dans cette figure qu'une fois que nous avons enlevé les données injectées (les faux signaux de pulsar), il n'y a aucun candidat significatif qui sort de "la ceinture bruyante" décrite dans la section 12. Les candidats à l'intérieur de "la ceinture bruyante" doivent être rejetés, car de tels candidats seraient produits par des artéfacts liés à la ligne de bruit du détecteur, comme discuté dans les sections 12 et 13. Il reste huit candidats survivants peu significatifs en dehors « de la ceinture bruyante », même après avoir déplacé les pulsars injectés. Ces candidats peu significatifs ont été éliminés par une analyse complémentaire en utilisant les données S4, ou par une identification en tant qu'artefact (par exemple un candidat s'est avéré être associé à un oscillateur de 70.12 hertz dans une des caisses électronique du VME reliées à l'interféromètre).
Nous concluons donc que nous n'avons vu aucune évidence plausible de signaux de pulsar dans la recherche Einstein@Home sur les données S3. Ceci n'est pas étonnant. Durant la série S3, les instruments LIGO étaient toujours dans leur phase de mise en service pour atteindre leur sensibilité de conception. Et même lorsque la sensibilité de conception sera atteinte, le niveau du bruit dans les instruments sera assez élevé pour venir obscurcir les signaux des ondes gravitationnelles présents dans les données.
Notre capacité à pouvoir détecter quelque chose dépendra à l'avenir de la nature, de la chance, et de notre capacité à améliorer nos méthodes de détection et d'analyse. Beaucoup de progrès ont été accomplis depuis l'analyse S3. Ces progrès et les perspectives à venir sont discutés dans la prochaine section.
15. Progrès depuis l'analyse de la S3 et perspectives pour les recherches futures ?
En juin 2005, nous avons commencé un nouveau cycle Einstein@Home avec une installation semblable, mais en utilisant des données (plus sensibles) issues du cycle scientifique LIGO S4. Une différence significative est que cette analyse S4 a utilisé des données issues des instruments du LIGO Hanford (H1) et du LIGO Livingston (L1). Cette première recherche sur les données S4 s'est terminée en décembre 2005, et a été utilisée en partie pour éliminer rétrospectivement une partie des candidats issus de la S3, comme mentionné dans la section 14.
Le 24 décembre 2005, nous avons lancé la recherche Einstein@Home amélioré (application albert) avec les données de la S4, et un certain nombre de modifications :
- Le format de la recherche utilise un paramètrage de l'espace métrique, ayant pour résultat une meilleure couverture des paramètres de l'espace (fournissant la sensibilité accrue).
- le temps d'intégration cohérent a été augmenté de 10 à 30 heures, ce qui a pour résultat une amélioration de la sensibilité de la contrainte d'environ de 70%.
- Une seule intégration logique est effectuée sur chaque ordinateur, sans étape de relation. La quantité de données retournées est contrôlée en retournant toujours et seulement les 13 000 candidats "les plus forts" de chaque unité de travail. Ceci empêche la ligne d'artéfact instrumental d'envahir les données des serveurs.
Cette recherche S4 améliorée s'est terminée en juin 2006, et le post-traitement des résultats est toujours en cours, bien qu'en majorité terminé. Les résultats seront annoncés dans un autre article semblable à celui-ci.
Alors que la recherche S4 améliorée se finissait en juin 2006, une nouvelle recherche avec la même installation a été lancée sur 840 heures de données des deux premiers mois de S5, analysés par segments de 30 heures (application einstein_S5R1). Après cinq ans de mise en service et d'améliorations continues, LIGO a atteint sa sensibilité de conception (« SRD ») dans le cycle de recherche S5 (voir la section 8), le traitement de ces données prendra environ un an et demi. Einstein@Home continuera les recherches améliorées sur ces données S5 lorsqu'elles seront disponibles. Notez qu'avec ces améliorations de la recherches E@H sur les données S4 et S5, il est attendu que le problème "de la ceinture bruyante" ("noisy belt") décrit dans la section 12 soit légèrement réduit, grâce à un temps d'intégration cohérent plus long (heures T=30 au lieu d'heures T=10) et d'un niveau de bruit amélioré pour améliorer la détection.
Ensuite, une autre longue phase scientifique est planifiée (S6), le laboratoire LIGO, la collaboration scientifique LIGO, et ses partenaires internationaux commenceront à installer une amélioration appelée Advanced LIGO [43], qui améliorera la sensibilité aux déformations par un facteur de 10. Comme le volume de l'espace qu'un instrument peut voir se développe au cube de la distance, cela signifie que le nombre de sources qui pourront être détectées sera jusqu'à 1.000 fois plus grand qu'avec le LIGO initial. Le nouveau matériel de détection sera installé dans le système existant du LIGO, au LIGO Hanford et à l'observatoire Livingston et remplacera les instruments actuels. Le LIGO avancé transformera la science des ondes gravitationnelles en un véritable outil d'observation. On prévoit que ces nouveaux instruments pourraient découvrir de nouvelles sources d'ondes gravitationnelles au moins une fois par jour, avec une force de signal excellente, qui permettra de lire et de détailler les formes d'onde qui seront comparées aux théories des étoiles à neutrons, des trous noirs, et des autres objets fortement relativistes.
16. Listes des participants à la collaboration scientifique LIGO S3
Ce rapport a été présenté le 4 Juillet 2005 par la collaboration scientifique LIGO (LSC) [ 8 ], grâce à la participation des scientifiques suivants [44]. Les publications scientifiques basées sur ce travail rendront également hommage à la contribution essentielle des participants à Einstein@Home.
La collaboration scientifique LIGO : http://www.ligo.org
Les auteurs remercient le soutien de la National Science Foundation pour la construction et la maintenance du laboratoire LIGO et le Particle Physics and Astronomy Research Council de Grande-Bretagne, l'institut Max-Planck et le land de Basse-Saxe/Allemagne pour le support dans la construction et la maintenance du détecteur GEO600. Les auteurs remercient également le soutien dans la recherche apporté par les agences et par le Conseil de recherche australien, le Conseil de recherches en sciences naturelles et en génie du Canada, et le Conseil scientifique de recherches industrielles en Inde, le département des sciences et des technologies en Inde, le ministère espagnol "Educación y Ciencia", la fondation John Simon Guggenheim, la Leverhulme Trust, la fondation David et Lucile Packard, la Research Corporation, et la fondation Alfred P. Sloan.
... fil 2.1
À la température ambiante (20°C) la densité du fil est de 11.35 grammes par cm3
... fréquence 5.1
La fréquence d'une onde gravitationnelle d'un pulsar est virtuellement constante lorsque la distance entre le détecteur et le pulsar ne change pas. Mais beaucoup de pulsars se trouvent dans des systèmes avec une étoile compagnon. Dans ces systèmes binaires, les deux étoiles gravitent l'une autour de l'autre. Dans ce cas, la distance entre le détecteur et le pulsar change constamment, ainsi la fréquence des ondes gravitationnelles du pulsar est modulée par le mouvement orbital, et n'a plus une fréquence fixe. Un autre exemple survient lorsqu'un pulsar tombe vers une concentration massive locale. L'accélération en résultant compliquerait quelque peu la forme des ondes gravitationnelles, présentant un décalage de la fréquence variant de façon linéaire avec le temps.
... Hz 5.2
C'est une simplification. En effet, si le pulsar émet des ondes gravitationnelles alors celles-ci emportent de l'énergie et la fréquence de rotation de l'étoile change - mais seulement très légèrement, ainsi pour le moment oublions cet effet.
... marche aléatoire 6.1
Un exemple de marche aléatoire souvent cité est le problème mathématique dit du "marin ivre". Un marin ivre marche sur une route en avançant et en reculant, changeant de direction au hasard. Après qu'une durée T, beaucoup plus longue que le temps de faire un pas, se soit écoulée, la distance moyenne (la racine carrée de la moyenne du carrée : rmsd) que le marin aura parcourue depuis le point de départ est proportionnelle à la racine carrée de T.
... instrument 9.1
Les artéfacts de lignes spectrales dont les origines ont été identifiées, par exemple, la résonance des lignes de transfert d'énergie électrique à 60 hertz, le mode violon des suspensions du miroir (résonnance haute fréquence : 343-347 hertz) et les résonances à 37 hertz résultant de l'imperfection de l'oscillateur synthétique utilisé pour moduler le laser.
... paramètres 10.1
![]() Amplitude des ondes gravitationnelles
Amplitude des ondes gravitationnelles
![]() Fréquence en Hz des ondes gravitationnelles (en Hz)
Fréquence en Hz des ondes gravitationnelles (en Hz)
![]() Angle d'inclination de l'axe de rotation du pulsar avec la ligne d'observation (en radians)
Angle d'inclination de l'axe de rotation du pulsar avec la ligne d'observation (en radians)
![]() Angle de polarisation de l'onde gravitationnelle (en radians)
Angle de polarisation de l'onde gravitationnelle (en radians)
![]() Phase initiale de l'onde gravitationnelle (en radians)
Phase initiale de l'onde gravitationnelle (en radians)
![]() Ascension droite du pulsar (en radians)
Ascension droite du pulsar (en radians)
![]() Déclinaison du pulsar (en radians)
Déclinaison du pulsar (en radians)
![]() Nombre de coïncidences prévues
Nombre de coïncidences prévues
Les définitions précises de ces paramètres (sauf pour ![]() ) sont données dans [38]
) sont données dans [38]
Le tableau suivant montre les propriétés des pulsars injectés matériellement (H et G) et avec un logiciel (S). Ces simulations de pulsars ont été injectés dans les données LIGO S3 comme si c'était des pulsars avec les propriétés suivantes :
| Nom du pulsar injecté | Fréquence [Hz] | Bande de signal [Hz] | déclination [radians] | Ascension droite [radians] |
| H0 | 265.5771052 | 0.1062 | -0.981180225 | 1.248816734 |
| H1 | 849.0832962 | 0.3396 | -0.514042406 | 0.652645832 |
| H2 | 575.163573 | 0.2301 | 0.060108958 | 3.7569288 |
| H3 | 108.8571594 | 0.0435 | -0.583578803 | 3.113188712 |
| H4 | 1403.163331 | 0.5613 | -0.217583646 | 4.886706854 |
| H5 | 52.80832436 | 0.0211 | -1.463269033 | 5.281831296 |
| H6 | 148.7190257 | 0.0595 | -1.14184021 | 6.261385269 |
| H7 | 1220.979581 | 0.4884 | -0.356930834 | 3.899512716 |
| H8 | 194.3083185 | 0.0777 | -0.583263151 | 6.132905166 |
| H9 | 763.8473165 | 0.3055 | 1.321032538 | 3.471208243 |
| G | 1125.647365 | 0.45026 | -0.616383646 | 0.776235274 |
| S1 | 344.2 | 0.1377 | 0.01 | 4.5 |
| S2 | 343.3 | 0.1373 | 0.01 | 4.5 |
| S3 | 342.4 | 0.1370 | 0.01 | 4.5 |
| S4 | 345.1 | 0.1380 | 0.01 | 4.5 |
| S5 | 346.01 | 0.1384 | 0.4 | 3.5 |
| S6 | 574.1 | 0.2296 | 0.0601 | 3.7569 |
- H : pulsars injectés matériellement ; S : pulsars injectés avec un logiciel; G : pulsars injecté matériellement dans les données LIGO, en liaison avec une injection matérielle pendant la dernière partie du S3 GEO.
- La colonne "Fréquence" liste les fréquences des ondes gravitationnelles des pulsars simulés.
- La troisième colonne "Bande de signal" liste les bandes de fréquences que le pulsar (simulé) pourrait influencer à la baisse ou à la hausse autour de sa fréquence. Du point de vue pratique, le pulsar entraîne un élargissement Doppler de fréquence quatre fois moins important que le mouvement de rotation de la terre autour du soleil, par exemple, 4
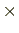 265,5771052
265,5771052 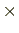 0,0001 = 0.1062 Hz pour le pulsar H0. Toutes les bandes de signal qui contiennent une injection matérielle ou logicielle ont été exclues dans la figure 14.1
0,0001 = 0.1062 Hz pour le pulsar H0. Toutes les bandes de signal qui contiennent une injection matérielle ou logicielle ont été exclues dans la figure 14.1 - L'ascension droite et la déclinaison sont données pour les coordonnées à l'équateur.