Source : First Results of RCN
La première étape du projet Rectilinear Crossing Number est accomplie. Le nombre minimum de croisements pour relier un ensemble de 18 points dans un graphe complet a été calculé avec succès :
le nombre minimal de croisements dans un graphe complet composé de 18 points (noeuds) est de 1029.
CR(18) = 1029
La disposition optimale des points est présentée ci-dessous :

Notez que ce schéma ne montre pas un graphe complet mais seulement sa structure. La raison est qu'on ne verrait rien si toutes les arêtes (C218=153) étaient dessinées. L'analyse de ce résultat est en cours, plus d'informations seront publiées dès que possible.
Ce résultat a été rendu public par un article dans le Frankfurter Allgemeine.
Voir l'article (en allemand)
Graphe complet - un défi pour les ordinateurs
Heinrich Hemme
 Les mathématiciens s'occupent souvent de problèmes qui semblent n'avoir aucune importance. Par exemple dans le domaine de la théorie des graphes.
Les mathématiciens s'occupent souvent de problèmes qui semblent n'avoir aucune importance. Par exemple dans le domaine de la théorie des graphes.
Un graphe est une figure constituée de points et de segments de droites reliant chacun de ces points. Les points sont appelés noeuds, et les segments de droite, des arêtes. Pour le mathématicien, la structure topologique des graphes n'a pas d'importance, seule compte la disposition exacte des éléments. On peut ainsi représenter les noeuds par des perles et les arêtes par des fils en caoutchouc. On peut disposer les perles et les fils à souhait, sans que le graphe change. Deux graphes peuvent paraître complétement différents, mais ces deux représentations différentes sont un seul et même graphe
Une analogie avec les segments conducteurs des circuits imprimés
Lorsque l'on y regarde de plus près, on peut faire la relation avec un circuit imprimé. Celui-ci est constitué de composants et d'une fine couche de cuivre, qui joue le rôle de segment conducteur entre les différents composants. Du point de vue mathématique, les segments conducteurs sont les arêtes du graphe et les points de soudure sont les noeuds.
Le fait de tracer précisement les lignes conductrices n'a pas d'importance, du moment qu'elles relient les composants correctement. Toutefois les "graphes" de circuits imprimés ne peuvent pas se croiser, car il y aurait des courts-circuits entre les lignes conductrices. En revanche, dans le cas - bidimensionnel - des graphes mathématiques, il peut y avoir des lignes qui se croisent, à savoir des jonctions des arêtes, et ceux-ci revêtent un intérêt tout particulier pour les théoriciens. En tentant de résoudre un de ces problèmes, ils ont atteint les limites des ordinateurs modernes.
Recherche : le nombre de croisements
Les mathématiciens se sont tournés vers un groupe bien particulier de graphes - les graphes rectilignes complets, dans lesquels chaque noeud est relié à chacun des autres noeuds par une arête. Ils se sont intéressés à trouver le plus petit nombre possible de croisements, et ce, à condition qu'aucune arête ne se superpose, qu'aucune arête ne passe 2 fois sur le même noeud et que pas plus de deux arêtes ne se coupent en un même point
On pourrait croire, si on simplifie trop le problème, qu'il est facile de déterminer le nombre de croisements pour un nombre de noeuds donnés. Mais c'est une erreur. En 1960, le célèbre mathématicien anglais Richard K. Guy, suite à un article publié dans la revue Nabla, avait sifflé l'ouverture de la chasse aux crossing numbers (nombres de croisements). Beaucoup de mathématiciens ont répondu à l'appel, mais les résultats ne furent pas prolifiques : jusqu'en l'an 2000, on avait seulement déterminé les nombres de croisements pour des graphes inférieurs ou égaux à neuf noeuds.
Les nombres de croissement en bref
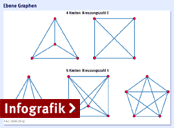
En principe, les graphes possédant un, deux ou trois noeuds peuvent avoir aucun point de croisement. Il est aussi possible de disposer quatre noeuds de telle sorte que les six arêtes ne se coupent nulle part dans le graphe. Ce n'est qu'avec un graphe avec cinq noeuds qu'il y aura au minimum un point de croisement. Plus le nombre de noeuds devient élevé et plus le nombre de croisements augmente rapidement : avec six noeuds, il s'élève à 3 ; avec sept noeuds : 9 ; avec huit noeuds : 19 ; et avec neuf noeuds : 36.
En 2000, Alex Brodsky, Stephane Durocher et Ellen Gether de l'université de la Colombie-Britannique à Vancouver, réussissaient enfin à découvrir le nombre de croisements pour les graphes à dix noeuds. Parallèlement, et avec une autre méthode Oswin Aichholzer, Franz Aurenhammer et Hannes Krasser de l'Université de technologie de Graz (Autriche) sont arrivés au même résultat.
Différentes formes
Le but premier des mathématiciens sous la direction de Aichholzer était tout autre. Ils voulaient déterminer les différentes formes de graphes complets, égaux et rectilignes pour un nombre donné de noeuds. Pour les graphes à un, deux ou trois noeuds, il n'y a respectivement qu'une seule forme. Il n'y a qu'avec les graphes avec quatre points que l'on obtient deux formes différentes. Les quatre noeuds prennent la forme d'un simple carré, et les six arêtes sont composées par les cotés du carré et ses 2 diagonales. Les diagonales se croisent en un point. Pour la seconde forme, trois noeuds sont reliés en formant les arêtes d'un triangle. Le quatrième noeud se trouve à l'intérieur de ce triangle. Les six arêtes ne se croisent pas dans ce graphe
Lorsque le nombre de noeuds augmente, le nombre de graphes augmente de façon exponentielle. Avec dix points, il existe déjà plus de 14 millions de graphes. Aichholzer et son groupe de recherche ont analysé tour à tour chacune de ces possibilités - dans certains cas comme sous-produit - ils ont trouvé que le plus petit nombre de croisements s'élevait à 62 et que seuls 2 de ces graphes arrivaient à cette solution. Toutes les autres formes de graphe ont plus de points de croisement. Encouragés par ce succès, ils ont appliqué leur procédure à des graphes avec onze noeuds. Ils ont trouvé plus de deux milliard de graphes différents et ont découvert que le nombre de croisements s'élèvait à 102.
Un réseau de 7500 ordinateurs
Avec ce résultat, la limite de la méthode a été atteinte. Le nombre de graphes différents avec plus de onze noeuds est si grand, que les ordinateurs les plus puissants au monde ne suffiraient plus pour tester toutes les solutions possibles. Mais Aichholzer et son groupe ont réussi à affiner la procédure de telle sorte qu'on puisse exclure d'emblée avec certitude une grande partie des formes qui ne pourront pas abriter la solution du nombre minimal de croisements.
Malgré cela, la puissance de calcul nécesaire à son étude est si grande, que l'Université Technique de Graz ne suffisait plus. Par conséquent, Aichholzer lança en 2004 le projet "Rectilinear Crossing Number". Chaque internaute pouvait apporter la puissance de calcul de son propre ordinateur (http://dist.ist.tugraz.at/cape5). Entre temps, plus de 7500 ordinateurs issus de 80 pays se sont joints au projet.
Un graphe avec 18 noeuds
La recherche allait bientôt devenir un succès. Durant les deux années suivantes, les nombres de croisements K pour les graphes allant de 12 à 17 noeuds pouvaient être calculés : K(12) = 153, K(13) = 229, K(14) = 324, K(15) = 447, K(16) = 603 et K(17) = 798. On était toutefois encore très éloigné d'une méthode générale, qui permettrait de calculer facilement le nombre de croisements pour un nombre de noeuds donné.
Toutefois, Aichholzer a réussi à développer des ressemblances, avec lesquelles on peut estimer les nombres minimaux de croisements. Puisqu'il a par exemple trouvé de cette façon les nombres de croisements pour des graphes avec 19 et 21 noeuds. Il a ainsi réussi à déterminer que K(19) = 1318 et K(21) = 2055. En décembre de l'année dernière, Aichholzer et son groupe ont enfin réussi à calculer le nombre de croisements pour le graphe à 18 noeuds. Pour trouver ce résultat, 10.000 jours de calcul processeur cumulés ont été nécessaires. Le nombre de croisements a été confirmé en janvier, il est égal à 1029.


