Connexion S'enregistrer

Nouvelles en VO

MOD_LNPD_MORE_CAT Nouvelles en VO  

Détails
Catégorie parente: Actualités

theSkyNet logo

Des problèmes récurrents liés à l’utilisation de Java ont perturbé le projet SourceFinder de theSkyNet.  Le bon fonctionnement du projet POGS sur la plate-forme BOINC a incité l’équipe de theSkyNet à planifier l’intégration de SourceFinder sur cette plate-forme, dans le courant de l’année. « Nous avions prévu une transition en douceur, mais hier, un problème technique a entraîné l’arrêt soudain et inattendu du serveur, » ont indiqué les scientifiques de theSkyNet.

Affichages : 4033

Lire la suite : theSkyNet stoppe l'application SourceFinder

Détails
Catégorie parente: Actualités

Constellation_ Logo

 

Le projet Constellation se dote de la nouvelle application Comet trails. « Après des essais réussis ces derniers mois, vous pourrez maintenant effectuer du calcul distribué et aider à prédire les tempêtes de météores pour les engins spatiaux ou les planètes, » ont annoncé les scientifiques de l'Aerospace research, mercredi.

 

Un financement de l'Agence spatiale européenne

L'Agence spatiale européenne (Esa) finance le projet Imex cometary trails de l'Institut des systèmes de l'espace (IRS), situé à l'Université de Stuttgart en Allemagne. Le but de l'application est de caractériser les traînées de poussières produites par les comètes dans le système solaire interne.

Affichages : 4745

Lire la suite : Constellation s’enrichit de l'application Comet trails

Détails
Catégorie parente: Les Projets BOINC

Le projet OGR27 a reçu sa dernière UT (unité de travail) le 19 février 2014 après 1821 jours d'activités !

Ce projet fait partie de la grille de calcul distributed.net mais nous pouvions y cruncher à travers l'équipe Yoyo@home (qui regroupait toutes les équipes BOINC).

Si l'on prend en compte le score de toutes les équipes BOINC (et donc le score de l'équipe Yoyo@home), la participation est de 5% du projet tout au long de ses 1821 jours et se score monte même à 10% sur la fin.

Si vous voulez voir les statistiques : http://stats.distributed.net/team/tlist.php?project_id=27&low=1&limit=100

Maintenant, il ne reste plus qu'à compiler les résultats afin de connaitre la règle de Golomb optimum pour 27 chiffres.

Les OGR ont de nombreuses applications dont entre autres : le positionnement des capteurs pour la cristallographie à rayons X, et la radioastronomie. Les règles de Golomb jouent également un rôle en combinatoire, en théorie du codage et dans les communications. Le docteur Golomb est l'un des premiers a avoir analysé leur utilité dans ces domaines.

Si maintenant vous voulez participer à l'aventure OGR28, rien de plus simple, il suffit de suivre le tuto pour rejoindre l'équipe de l'AF sur Yoyo@home et pour ceux qui ont déjà participé à OGR27 le changement se fait automatiquement !

 

Bon crunch !

Affichages : 12068

Détails
Catégorie parente: Actualités

article traduit par Ryzen

Le cadre du projet Harvard Clean Energy permet d'évaluer le calcul de structures candidates pour les matériaux électroniques organiques - en particulier le photovoltaïque - à une échelle sans précédent. Nous rapportons les composés les plus prometteurs qui ont émergé après étude de 2,3 millions de sujets moléculaires au moyen de 150 millions de calculs basés sur la théorie fonctionnelle de la densité. Nos meilleurs candidats sont analysés quant à leur composition structurelle afin d'identifier les éléments importants et d'extraire les règles de conception des matériaux efficaces. Une base de données en ligne des résultats est mis à la disposition de la communauté.

Affichages : 3789

Lire la suite : Harvard Clean Energy Project

Détails
Catégorie parente: Les Infos

9-1Un nouveau sous-projet mathématique sur yoyo@home:

ODD WEIRD SEARCH ou À la recherche des nombres étranges impairs !

Serez vous le premier à en découvrir un ? Enfin... s'ils existent ! Pour le savoir, une seule façon: commencer les calculs. Toutes les infos ici.

Affichages : 3268

Détails
Catégorie parente: Actualités

yoyo

Odd Weird Search

Recherche de nombres étranges impairs

 

 INSCRIPTION Windows Linux

Télécharger BOINC (tutorial)

URL du projet : http://www.rechenkraft.net/yoyo

Applications :  Windows et Linux 64 bits

Liens du Projet
L'Alliance Francophone
Statistiques

Administré par Yoyo et l'équipe allemande Rechenkraft.net, yoyo@home est une plateforme multi-projets qui permet de faire fonctionner des programmes de recherches extérieurs à BOINC. Pour ce faire, Yoyo et son équipe de programmeurs adaptent les applications au format BOINC.

Outre celui-ci, yoyo@home permet pour le moment de participer au choix à d'autres projets tels que Evolution@home (l'évolution des espèces), Muon (accélérateur de particules partagé), ECM (factorisation en courbe elliptique de Lenstra pour trouver des facteurs de différents nombres) ou encore OGR-27 (déterminer la façon optimale de placer 27 marques selon la règle de Golomb).

Le choix des projets s'effectue sur la page de votre compte dans vos préférences Yoyo@home > (appuyer sur Edit yoyo@home preferences, puis cocher ou décocher les cases à souhait).

 

9-1Odd Weird Search est le projet de la théorie des nombres qui recherche des nombres étranges.

Qu'est ce qu'un nombre étrange ?

Pour un entier naturel N, si la somme de tous ses diviseurs (y compris 1 mais pas N) est plus grande que lui, alors il est appelé "nombre abondant".

Par exemples:

  • 8 n'est pas un nombre abondant car ses diviseurs (1, 2 et 4) dont la somme qui vaut 1+2+4 = 7 est inférieur à 8.
  • 12 est un nombre abondant car la somme de ses diviseurs qui vaut 1+2+3+4+6 = 16 est supérieur à 12.

Un nombre abondant est un nombre étrange si aucune somme de ses diviseurs est égale à lui même.

Par exemples:

  • 12 est abondant mais pas étrange car 1+2+3 +4 +6 = 12.
  • 70 est un nombre étrange (le plus petit) car la somme de ses diviseurs vaut 1+2+5+7+10+14+15 = 74 (74>70) et aucune somme de ses diviseurs ne vaut 70 (il faudrait retrancher 4 à la somme de ses diviseurs mais 4 est impossible à produire avec ceux-ci).

Une page de l'OEIS (On-Line Encyclopedia of Integer Sequences) est consacrée à ces nombres étranges. Elle contient une liste des nombres étranges connus. Il est à noter que chaque nombre dans la liste est pair.

En fait, aucun nombre étrange impair est connu. Les précédents efforts de recherche ont été menés jusqu'à 1017. Le grand mathématicien Paul Erdos a offert une récompense de 10$ pour la découverte d'un nombre étrange impair et de 25$ pour la démonstration de 'absence de nombre étrange impair. On en déduit qu'Erdos pensait qu'il était plus probable qu'ils existent et que le problème était suffisamment intéressant pour promettre une récompense !

Il a été montré qu'une infinité de nombres étranges existe. Le fait que la suite de nombres étranges a une densité asymptotique (en) positive a aussi été démontré.

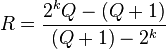En 2012, aucun nombre étrange impair n'a encore été découvert. S'il en existe, ils doivent être plus grands que 232 ≈ 4 × 109. Stanley Kravitz a démontré que si k est un entier strictement positif, si Q est un nombre premier et si R=frac{2^kQ-(Q+1)}{(Q+1)-2^k} est aussi un nombre premier, alors l'entier n=2^{k-1}QR est un nombre étrange.

À l'aide de cette formule, il a trouvé le plus grand nombre étrange connu actuellement :

n=2^{56}(2^{61}-1)153722867280912929approx2cdot10^{52}

Le projet poursuit l'effort de recherche des numéros étranges impairs jusqu'à 1020 ou 3.1020, ou même 1021. Le temps CPU pour tester jusqu'à 1020 serait d'environ 26,3 années, y compris le facteur de duplication des résultats pour vérification.


Sources:

 

 

Affichages : 5764
  1. Mindmodeling@home : remerciement des admins du projet
  2. World Community Grid – Mises à jour importantes
  3. OProject@home
  4. FightMalaria@Home : premier succès
  5. Rejoindre Ibercivis et aider avec le projet Bindsurf
  6. Nouvelle version de boinc

Page 33 sur 35