
Suite à une publication parue sur le site de Docking@Home en avril concernant le processus de recherche et les résultats de la méthode de calcul, vous trouverez ci-dessous le document traduit en français.
RÉSUMÉ
Les simulations d'amarrage sont couramment utilisées pour comprendre l’attache des médicaments mais elles nécessitent la recherche d'un grand volume de conformations protéine-ligand. Le calcul distribué permet de calculer des simulations d'amarrage par informatique à un tarif jamais vu auparavant, mais dans un même temps le besoin de scientifiques pour faire face à ces données est plus important. En analysant ces ensembles de données, une pratique commune consiste à réduire le nombre résultant de candidats de 10 à 100 conformations basées sur des valeurs d'énergie et laisser la tâche fastidieuse aux scientifiques de sélectionner subjectivement un possible ligand quasi-native. Les scientifiques effectuent normalement cette tâche manuellement à l'aide d'outils visuels. Non seulement le processus manuel dépend toujours de résultats d'énergie imprécis, mais peut aussi être fortement prédisposé aux erreurs.
Les contributions de ce papier sont double: d'abord, nous aborderons le problème du volume de recherche concernant les conformations protéine-ligand, appuyées par le projet de calcul bénévole Docking@Home (D@H). Deuxièmement, nous aborderons le problème de la précision, et automatiquement, de la sélection de ligand quasi-native parmi le grand nombre de résultats D@H en utilisant une classification probabiliste hiérarchique basée sur la géométrie ligand. Notre méthode soutient que, même lorsque nous testons une recherche qui n'est pas biaisée par le fait de partir de conformations ligand quasi-native, elle surpasse nettement les méthodes basées sur l'énergie.
1. INTRODUCTION
La conception de nouveaux médicaments repose sur la recherche de petites molécules, appelées ligands, qui s’amarrent aux protéines et jouent un rôle essentiel dans l’activation ou la désactivation des fonctions de celles-ci. L'étude des interactions protéine-ligand dans les laboratoires est extrêmement coûteuse en temps et exigeant en particulier pour la détermination de la structure expérimentale par cristallographie aux rayons X et résonance magnétique nucléaire (RMN). Des simulations sur ordinateur sont utilisées pour accélérer ce processus et réduire les coûts. La recherche informatique pour les médicaments putatifs (c'est-à-dire des ligands qui accostent bien dans une protéine) est une recherche incertaine car il existe un très grand volume de conformations possibles d'accueil, ce volume est formé par la protéine, le ligand, les méthodes de calcul, et les degrés de liberté voulant être explorées [11].
Afin d'explorer un vaste volume, les scientifiques peuvent compter sur les technologies de calcul distribué, telles que le cloud computing et le calcul bénévole. Ces technologies peuvent effectuer de coûteuses simulations de calcul protéine-ligand à un rythme jamais vu auparavant. Dans le même temps, cette capacité conduit à des ensembles de données de simulation de plus en plus grands, ce qui entraîne de nouveaux défis pour les scientifiques qui ont pour but d’analyser ces données. Particulièrement, dans ses simulations d’accueil cela aboutit à l'analyse de très vaste jeu de conformations ligand amarrées dans une protéine. En plus de la taille des données, les scientifiques doivent relever le défi de la sélection de ligands sous l'incertitude. Les enchainements d'amarrage protéine-ligand sont normalement basés sur des valeurs d'énergie rapprochées. Malheureusement, ces estimations d'énergie peuvent être inexactes; en d'autres termes les conformations d'énergie minimale ne correspondent pas toujours à la bonne conformation quasi-native. Ainsi, le choix de la bonne conformation des ligands quasi-natives d'un vaste ensemble de conformations est un processus de sélection incertain.
Lorsqu'il s'agit d’analyser de grands ensembles de données ligand, une pratique courante consiste à réduire le nombre de candidats de 10 à 100 conformations fondée sur des valeurs énergétique et laisser ensuite aux scientifiques la tâche fastidieuse de sélectionner subjectivement un ligand quasi-native possible. Les scientifiques effectuent normalement cette tâche manuellement à l'aide d'outils visuels tels que VMD [10] ou Chimera [5]. Non seulement le processus manuel dépend toujours de résultats d'énergie imprécis, mais il peut aussi être fortement prédisposé aux erreurs. Au meilleur de nos connaissances, la plupart des méthodes avancées de traitement de cette tâche ne sont pas entièrement automatisé et il y a toujours un besoin d'amélioration de la méthodologie et de l'automatisation de ce processus.
Les contributions de ce papier sont double: d'abord, nous aborderons le problème de la taille de l’espace de recherche concernant les conformations protéine-ligand, appuyées par le projet de calcul bénévole Docking @ Home (D @ H). Deuxièmement, nous aborderons le problème de la précision, et automatiquement, la sélection de ligand quasi-native parmi le grand nombre de résultats D @ H. Dans cet article nous:
• Utilisons le calcul bénévole du projet D@H visant à recueillir les résultats de simulation de deux différents algorithmes d’amarrage (chacun avec différents niveaux de précision pour la représentation des solvants) et deux approches différentes pour générer des conformations ligand initiales.
• Présentons une méthodologie de regroupement qui permet une analyse précise et efficace de la grande base de données, même en présence de l'incertitude des données. Notre méthode utilise une classification probabiliste hiérarchique qui organise efficacement les structures ligand dans un nombre variable d'ensembles en fonction de leur géométrie.
• Utilisons notre méthode pour identifier avec moins d'incertitude, le vaste ensemble de données recueillies par D @ H et nous sélectionnons une structure unique de ligand qui représente potentiellement le meilleur candidat à une conformation quasi-native.
• Prouvons empiriquement que notre méthode est insensible aux différentes protéines, aux algorithmes d’amarrage, des conditions de démarrage et en moyenne, elle fournit une solution précise quasi-native dans 85% des cas examinés dans ce travail.
Le reste de cet article est organisé comme suit: La section 2 présente comment D@H explore le vaste espace de conformations ligand. La section 3 introduit le problème de la précision de la sélection des conformations quasi-native. La section 4 décrit notre réseau probabiliste hiérarchique et comment l'utiliser pour analyser de grandes séries de données d'amarrage protéine-ligand. Le chapitre 5 présente nos résultats avec une comparaison d'une méthode plus traditionnelle pour la sélection des conformations quasi-native. La section 6 parlera des discussions liées au travail et l'article 7 conclura le dossier.

2- Explorer le vaste espace de conformations des molécules ligand avec Docking@Home
(D@H) est un projet de calcul bénévole visant à construire par le calcul distribué un environnement propice afin d’aider les scientifiques à mieux comprendre les interactions protéine-ligand. En choisissant avec précision les détails atomiques ainsi que les structures de ligand. D@H utilise des milliers d’ordinateurs bénévoles pour simuler le comportement de ces petites molécules (appelées ligand) lors de leur amarrage au sein d’une protéine et ainsi contrôler leurs fonctions. D@H s'appuie sur BOINC [1] (Berkeley Middleware Open Infrastructure for Network Computing) qui génère, distribue et réceptionne les données par internet. Au sujet plus particulier de Docking@Home, celui-ci distribue les travaux contenant un ligand et une protéine aux machines bénévoles (également appelées clients D@H). La simulation d'amarrage est effectuée sur l’ordinateur-hôte, qui, à la fin du calcul, retourne la conformation du ligand, lorsque celle-ci s'est amarrée dans la protéine. Par conformation de ligand, nous entendons la position tridimensionnelle des atomes de ligand et leurs interactions avec la protéine. Actuellement, D@H est pris en charge par environ 12'000 à 30'000 bénévoles et leurs ordinateurs; D@H a récupéré plus de 2TBytes de données en six mois et a recueillis quotidiennement environ 30’000 résultats d'amarrage. Ceux-ci sont stockés dans un référentiel et analysés par la suite, ainsi nous sélectionnons parmi des millions de candidats un ensemble très réduit de conformations du ligand en se basant sur la probabilité de la convergence de l'algorithme d'amarrage.
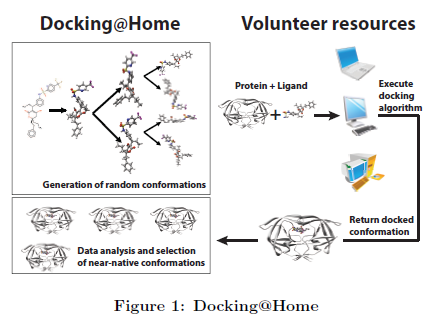
Le solvant, usuellement de l'eau, dans lequel les complexes protéine-ligand résident, a une influence fondamentale sur les interactions de celles-ci dans toute simulation d'amarrage. Le solvant agit sur les interactions électrostatiques de dépistage et au sein des atomes dans la structure moléculaire. D@H utilise deux algorithmes d'amarrage avec différentes formes du solvant:
• Méthode 1: Une représentation implicite de l'eau est utilisée avec un coefficient diélectrique dépendant de la distance (faible si la distance entre les atomes est étroite et progressivement plus grande si la distance est croissante)
• Méthode 2: Une représentation implicite plus physiquement précise de l'eau est utilisée à l'aide d'un modèle quasi-authentique.
La méthode basée sur le modèle quasi-authentique est plus intensive pour le CPU et la mémoire. En même temps elle fournit une description physiquement plus précise du potentiel de l'énergie d'un ligand à l’endroit précis de la conformation de celle-ci, lorsqu’elle est exposée au solvant. Dans de nombreuses situations, où une grande partie du ligand est exposé au solvant, le modèle authentique devrait contribuer significativement à fournir la meilleure conformation du ligand (par exemple lorsqu'une orientation d'un ligand donnée laisse un groupe volumineux hydrophobe exposé au solvant, cela la pénalise, exposer un groupe hydrophile comme un groupe hydroxyle OH au solvant est beaucoup plus favorable). Les travaux récents (de Rahaman, Armen, Estrada, Taufer et Brooks) afin de comparer l'exactitude de la méthode 1 et la fabrication des molécules de la méthode 2 ont démontré que la mise en œuvre particulière utilisée dans ce travail a des performances plus pauvres pour distinguer les modèles quasi-authentiques au niveau géométrique. Cette observation est similaire à celle observée par les calculs effectués sous Boinc. Les créations de molécules quasi-authentiques de la méthode généralisée sont capables d’être plus performantes que la méthode 1. Toutefois, dans le scénario actuel, même compte tenu de la précision moindre de la méthode 2, nous démontrons que notre regroupement hiérarchique probabiliste est en mesure de façon significative d’améliorer la discrimination des conformations quasi-native, même compte tenu de l'incertitude inhérente de la fonction pour la méthode 2.
D@H cible trois protéines différentes : la trypsine, le VIH et p38 Alpha. Ces protéines ont été sélectionnées parce qu’elles se caractérisent par différents degrés de flexibilité au cours du processus d'amarrage. La trypsine [7] est une protéase relativement rigide qui brise les autres protéines dans le système digestif. Des études récentes suggèrent que les inhibiteurs de la trypsine peuvent avoir des applications potentielles dans le traitement du cancer du sein. Il a été observé que la trypsine active les récepteurs des protéases (protéine dans la membrane de la cellule tumorale). Lors de ce processus, la protéine provoque la dégradation de la matrice extracellulaire, résultant de la propagation de la cellule tumorale d’un endroit à l'autre (métastases). Des médicaments peuvent agir comme inhibiteur en désactivant la trypsine protéase et sont donc des agents potentiels capables d'arrêter la propagation du cancer du sein. La protéase du VIH (VIH PR) [2] est une protéine relativement flexible au sein de la molécule du VIH et est essentielle à sa réplication dans les cellules humaines. Au cours du processus de construction du virus VIH à l'intérieur de la cellule humaine, le VIH PR Clive, nouvellement synthétisé pourrait s’accrocher au sein de la molécule en ciblant le génome infecté. Ce processus est nécessaire pour construire un virus VIH mature. Le VIH PR est une cible thérapeutique- bien connue pour le traitement de l'infection au VIH et afin de prévenir l'apparition du sida chez les patients déjà infectés. Un médicament qui peut se lier étroitement à la molécule active inhibera significativement l'activité enzymatique d’une importante population de molécules de VIH PR et réduire massivement le processus de réplication virale dans les cellules infectées. Ces médicaments sont appelés des inhibiteurs de protéase. Plusieurs inhibiteurs de protéase, comme saquinavir, ritonavir, indinavir, et Nelfinavir sont disponibles pour le traitement de l'infection par le VIH.

3- Sélection de conformations quasi-native sous incertitude
L’amarrage protéine-ligand utilise des méthodes d’évaluation distinctes pour deux tâches : la première étape est la discrimination de la géométrie de liaison du ligand (l'identification de conformations quasi-natales) et la deuxième étape est une comparaison de ligands différents (d’espèce chimique différente) pour prévoir quel ligand se lie le mieux à la protéine. D@H est un moteur pour la première étape et les résultats pour la deuxième étape peuvent être réalisés dans une étape post-traitement. Cet article ne se concentre pas sur la deuxième étape, mais est entièrement concentré sur la première.
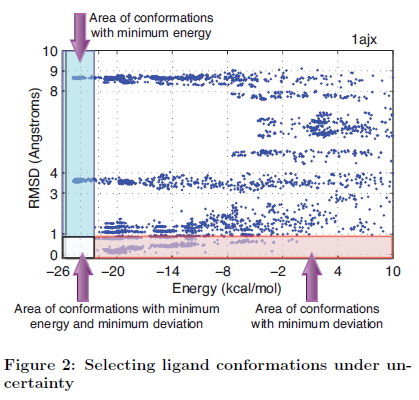
Tout en s’occupant de la méthode de notation, nous avons initialement compté sur une approche d’évaluation traditionnelle basée sur des valeurs d'énergie : nous avons choisi des ligands avec une énergie faible comme les conformations quasi-natales les plus probables. Nous avons immédiatement identifié les insuffisances de cette approche en termes d'exactitude. La figure 2 montre un exemple de 100,000 conformations ligand (chaque point dans la figure est une conformation ligand) obtenu avec Docking@Home pour le complexe 1ajx. Ici, les conformations ligand sont marquées par leur énergie potentielle (abscisse) et leur "Racine Carrée Moyenne Ecart-type" (RMSD) en ce qui concerne la structure cristalline connue (l'axe des ordonnées). Le RMSD est mesuré en Angströms (°A) et est calculé par la racine carré de la moyenne de la différence élevée au carré de tout atomes de ligand non-hydrogène dans la simulation de conformation ligand et les atomes de ligand dans la structure cristalline. La figure montre trois régions de pertinence : (1) Le secteur de conformations avec l'énergie minimale, qui est le rectangle vertical qui va de-26 à -22 kcal/mol. Une conformation ligand avec l'énergie minimale ne fait pas toujours une conformation quasi-natale. Les conformations dans ce secteur seraient choisies par une méthode qui représente seulement l'énergie et il y aurait des chances que ces candidats ne soient pas des conformations quasi-natales. Dans la figure nous pouvons voir deux secteurs de minimums entre 3-4°A et 8-9°A. (2) Le secteur de conformations avec un écart minimal (RMSD). Le RMSD est calculée par rapport à la structure cristalline, comme expliqué ci-dessus. Ce secteur est noté par le rectangle horizontal qui va de 0 à 1 °A. Idéalement, l’évaluation minimum d'une fonction avec une importante exactitude se trouverait dans ce secteur. Cependant, le minimum global n'est pas toujours trouvé (c'est le cas dans la Figure 3). Pour la découverte de nouveaux médicaments, la dimension d'écart (l'axe des ordonnées) est inconnue et ne peut pas être utilisée pour choisir le candidat de conformation de ligand. Dans cet article nous supposons que cette restriction se tient toujours et nous utilisons le RMSD seulement pour des buts de validation. (3) est le secteur de conformations avec l'énergie et l'écart minimal, qui est l'intersection des deux autres secteurs décrits auparavant. Idéalement ce secteur devrait être très peuplé pour augmenter les chances de choisir le bon candidat de conformation de ligand. Comme le montre la figure, ce n'est pas le cas, l'augmentation du niveau d'incertitude permet de rendre plus difficile la sélection des candidats ligand quasi-native.
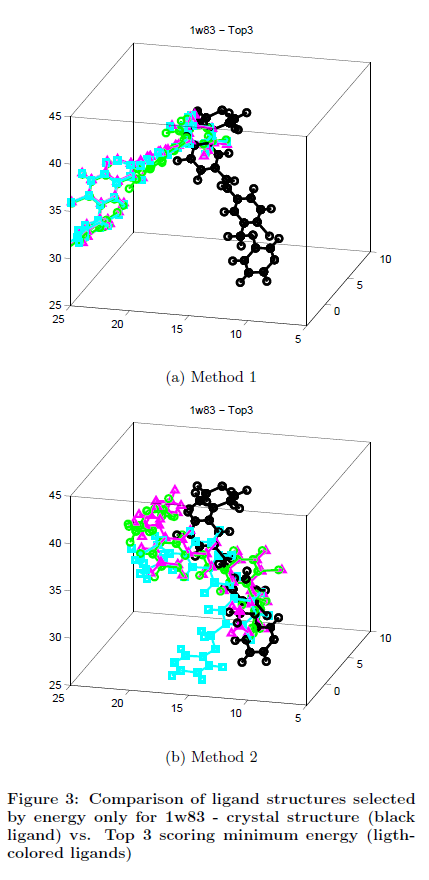
Nous avons observé le problème à travers les résultats d’amarrage générés par les deux différentes méthodes pour les trois protéines et les différents ligands considérés. La figure 3 montre un exemple de ce phénomène. 1w83 est la p38alpha kinase dans un complexe avec une petite molécule inhibitrice (ligand). Les deux sous-figures, 3.a et 3.b, montrent la comparaison graphique de la 1w83 seul ligand dans la structure cristalline (ligand noir) par rapport au top 3 des conformations ligand marqué par le minimum d'énergie sur l'ensemble des échantillons D H @ pour ce complexe (ligands gris). La figure 3.a correspond à la conformation ligand produit par la méthode 1. Il s'agit d'un cas extrême où la fonction de notation attribue le plus bas de l'énergie à une série de conformations qui convergent avec une orientation nettement différente de la structure cristalline. Figure 3.b correspond à la conformation ligand produit par la méthode 2 pour le même complexe. Cette figure montre que le minimum d'énergie des structures ne convergent pas vers une solution unique en dépit du grand nombre d'échantillons D H @. Dans le même temps, ces trois résultats sont sensiblement différents entre eux et aucun d'eux n'est suffisamment précis pour être appelé une conformation quasi-native.
Nous excluons que le problème d’incertitude de notation est liée à un échantillonnage insuffisant ou inefficace de l'espace de travail: D @ H est en effet capable d'échantillonnage intensif de l'espace d’étude. D'autre part, la modélisation des énergies est encore imprécise, même en utilisant la méthode basée sur le Generalized Born modèle du solvant implicite.

4- Un algorithme de regroupement probabiliste et hiérarchique
Les résultats de la section 3 soulèvent une question importante. Compte tenu de l'inexactitude des algorithmes d'accueil et des millions de conformations recueillis, comment les scientifiques peuvent-ils choisir ceux qui sont plus susceptibles de se produire dans la nature, étant donné que l'énergie n'est pas toujours une mesure d’évaluation fiable?
Les algorithmes de classification peuvent être utilisés pour affiner les données avec succès dans les phases de post-traitement. Ils peuvent également être utilisés pour identifier les résultats qui sont représentatifs des solutions dans les simulations. Les algorithmes de regroupement peuvent être partitionnels ou hiérarchiques. Un regroupement partitionnel divise les données selon une mesure de distance. Une limite importante de cette famille d'algorithmes, est que lorsqu'il est utilisé avec des données telles que les conformations protéine-ligand recueillies dans D @ H, le nombre de clusters doit être connue a priori. Dans D @ H, ce nombre n'est pas connu et une estimation précise et efficace de ce nombre n'est pas possible ni quand la simulation est en cours, ni quand la simulation est terminée et que tous les résultats sont collectés. D'autre part, les algorithmes de classification hiérarchique n'ont pas besoin de connaissances préalables sur le nombre final de clusters et peuvent être classés en agglomération ou en division. Un cluster hiérarchique ascendant commence avec chaque élément comme un groupe particulier, puis fusionne des éléments similaires dans de grosses grappes. Un algorithme hiérarchique de division commence avec un seul groupe comprenant toutes les données et les répartit ensuite en fonction d'une certaine distance métrique. Le défi pour la classification hiérarchique consiste à déterminer la meilleure profondeur de regroupement, c'est à dire, savoir quand arrêter la fusion ou la division des clusters. Une autre condition importante pour l'utilisation de toute méthode de classification est la capacité d'organiser automatiquement les données sans avoir toutes les données déjà classées, étiquetées, ou annotées et sans intervention humaine.
De toute évidence, aucune des techniques de clustering ci-dessus ne propose un champ d'application de manière efficace et précis de regroupement des ensembles de données tels que les résultats de D @ H, quand ils sont pris individuellement. Par conséquent, plutôt que d'utiliser une technique de clustering unique, nous proposons de combiner deux techniques pour tirer parti de leurs points forts. En particulier, nous proposons d'utiliser un cadre probabiliste hiérarchique qui combine (1) la capacité de faire face à l'incertitude des données en utilisant un fuzzy (clustering avec partitionnement) (2) la capacité d'identifier le nombre de grappes nécessaires à l'exécution en utilisant un algorithme de division hiérarchique pour lequel la hiérarchie cluster-profondeur est déterminée de manière probabiliste basée sur la variabilité du résultat. Plutôt que d'utiliser les énergies, nous utilisons les conformations géométriques des ligands comme entrée à notre regroupement et le RMSD entre les résultats des ligands D @ H et la distance métrique. Notez qu'ici nous nous référons à la RMSD comme mesure pour comparer les résultats de ligands entre eux et nous ne nous référons pas à la structure cristalline qui est inconnu pour nous pendant le processus d’évaluation. Nous supposons également que D @ H nous donne le nombre suffisant d'échantillons, et ainsi s’approcher vers des solutions de simulations quasi-native. Notre structure hiérarchique probabiliste est en mesure d'effectuer un regroupement efficace sans surveillance des grands ensembles de données de D @ H, même en présence d'incertitude.
Pour être plus précis, le Partitionnement Moyen Flou (Fuzzy C-Means (FCM)) [4] permet un partitionnement non disjoint des données, permettant de traiter les incertitudes. Dans un partitionnement traditionnel, chaque élément appartient à un seul groupe de données ; au contraire, dans un partitionnement flou chaque élément a un score, ou degré d’appartenance à chacun des groupes de données. Les éléments appartiennent à chaque groupe avec un degré différent dépendant de leur distance au centre (appelé également centroïde) de ce groupe.
Plus formellement, pour chaque ensemble de données D et chaque élément di appartenant à D, on détermine un vecteur score si donnant la probabilité que di soit un élément de chaque partitionnement : si = si ,1,si ,2,…si ,k où k est le nombre prédéfini de partitions et où la somme des si vaut 1. FCM est un algorithme récursif : on commence par sélectionner k éléments au hasard (appelé centroïdes initiaux) dans le jeu de données D. La seconde étape est de calculer le vecteur score si pour chaque élément di, où le degré d’appartenance est l’inverse normalisé de la distance au centroïde Ck (voir équation 1), la distance(x,y) étant une fonction personnalisée qui peut être ajustée selon le type de données traitées. Pour chaque groupe, un nouveau centroïde C’k est calculé comme étant la moyenne de tous les points pondérés par leur degré d’appartenance au groupe (voir équation 2). Ce procédé est réitéré jusqu’à la stabilisation des centroïdes, c'est-à-dire jusqu’à ce qu’ils restent inchangés.
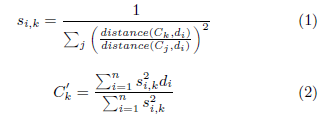
Dans notre architecture, FCM travaille de concert avec un algorithme de partitionnement hiérarchique des données. Cet algorithme commence avec un jeu de données Dm (m≠0) et utilise FCM pour le diviser en deux sous-ensembles (k=2), l’un étant défini comme le complément de l’autre (Dm+1 et D-Dm+1). Les éléments redondants (ceux n’appartenant pas fortement à un sous-ensemble ou l’autre) étant éliminés temporairement de ces deux partitions. Notre algorithme hiérarchique probabiliste sélectionne la partition (Dm+1) avec une probabilité proportionnelle à sa taille et inversement proportionnelle à sa variance interne. Cette partition est ensuite utilisée pour les partitionnements suivants. Le processus continue jusqu’à ce que la moyenne des deux partitions (Dm+1 et D- Dm+1) soit égale avec une significativité statistique de 0.05. Pour déterminer si les moyennes des groupes sont égales, nous utilisons le t-test de Welch [19] tel que montré dans l’équation 3, où Cm+1 est le centroïde de Dm+1, Cm’+1 est le centroïde de Dm- Dm+1, et σm+1 et σm’+1 sont leurs déviation standard respectives. Une fois le t-test calculé, nous trouvons sa p-value d’après une t-distribution de Student [17]. On sauvegarde les centroïdes et continue la partition jusqu’à ce que la p-value soit inférieure à 0.05 et que le nombre d’éléments de Dm+1 reste plus grand qu’un seuil défini par la précision souhaitée (par exemple 1 Angström). A chaque étape, la hiérarchie des centroïdes est conservée et utilisée comme résumé de l’espace des données.
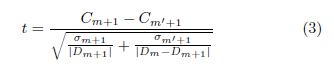
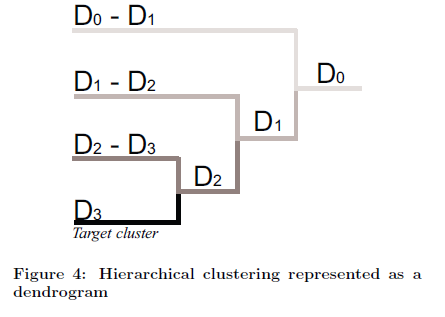
Notre architecture de partitionnement probabiliste hiérarchique peut être utilisées pour (1) organiser automatiquement des données en jeux disjoints (2) trouver une solution globale, probablement unique, à partir de résultats multiples indépendants. La figure 4 présente un exemple pour lequel l’algorithme hiérarchique est représenté graphiquement comme une structure arborescente (dendrogramme). Pour cette figure particulière, les centroïdes pour D0, D0-D1, D1, D1-D2, D2, D2-D3, et D3 sont déterminés et peuvent être utilisés pour résumer et analyser les différentes dimensions du jeu de données. Par définition, le dernier groupe est également le plus compact (c'est-à-dire le plus grand avec la plus petite variance interne). En conséquence, le centroïde D3 peut être utilisé comme solution la plus probable de l’ensemble de données.

5- Précision des mesures de DOCKING
Pour tester notre cadre probabiliste hiérarchique, nous avons réalisé des essais « d’accueil » pour chacun des 23 complexes protéine-ligand de la protéase du VIH (c.-à-1ajv, 1ajx, 1d4h, 1d4i, 1d4j, 1ebw, 1ebz, 1g2k, 1g35, 1gno, 1hbv, 1hih, 1hps, 1hpx, 1hsg, 1htf, 1hvi, 1hvj, 1hvk, 1iiq, 1m0b, 1ohr, et 1T7K), 21 ligands d'accueil dans la protéine trypsine (c.-à-1c2d, 1c5p, 1c5q, 1ce5, 1g36, 1GHz, 1gi4, 1gi6, 1gj6, 1k1i, 1k1j, 1k1l, 1k1m, 1k1n, 1ppc, 1pph, 1qb6, 1tpp, 1xug, 2bza, 3ptb), et 12 ligands d'accueil dans la kinase P38alpha (c.-à-1a9u, 1bl6, 1bl7, 1di9, 1kv1, 1kv2, 1ouk, 1ouy, 1oz1, 1w83, 1w84, 1yqj). Pour chacun de ces complexes nous avons réalisé 2 millions d’essais.
Dans une première série de tests afin d'évaluer si nos groupes probabilistes hiérarchiques tiennent la route et peuvent capturer des conformations quasi-native indépendamment de la méthode d'accostage, nous avons considéré les deux méthodes d'accueil décrites à la section 3 (méthode 1 et 2) et généré de façon aléatoire des ligands comme des conformations initiales (voir les figures 5 et 6). Dans une deuxième série de tests, on a évalué si les configurations initiales utilisées dans le procédé d'accueil jouent un rôle actif dans la polarisation de l'exactitude de notre sélection de groupe de base, nous avons utilisé la méthode 1 et les ligands définis par l'utilisateur dont les conformations sont > 5 Angstroms à partir de la structure cristalline correct (voir figure 7). Notez que la conformation avec > 5 Angstroms des structures cristallines correspondantes est considérée comme une mauvaise conformation.
Nous avons utilisé notre groupe probabiliste hiérarchique pour trouver les conformations de ligands les plus susceptibles d’être quasi-native pour chaque complexe. Pour chaque complexe, notre cadre d’étude c’est réalisé sur 100.000 conformations de ligands. La distance métrique utilisée pour grouper chaque ligand est le RMSD de ses coordonnées atomiques contre tous les autres ligands déjà dans le groupe. Si une simulation converge, alors le plus grand groupe avec une variance interne inférieure (notée comme un groupe cible) est probablement le groupe qui contient le plus de conformations quasi-native. Dans nos expériences, la conformation ligand avec le plus haut degré d'appartenance (centroïde) pour le groupe cible est sélectionnée comme notre prédiction quasi-native (voir équation 1). Dans le reste de cet article, nous nous référons à cette conformation comme le regroupement candidat d’un complexe donné.
L'ensemble du processus de regroupement et de sélection du groupe candidat a été réalisé sans l'aide des structures cristallines disponibles pour les complexes de BDPT [15]. Les structures cristallines ne jouent un rôle important que dans la phase de validation de notre cadre quand, pour chaque complexe, nous avons calculé le RMSD du groupe candidat à l'égard de sa structure cristalline.
Une conformation peut être considérée comme une conformation quasi-native si son RMSD est inférieure ou égale à deux Angstroms, mais des conformations RMSD entre deux et trois Angstroms sont considérées des résultats intéressants. Dans le cas de l'approche énergétique, nous considérons que nous capturons une conformation quasi-native si la médiane arithmétique est inférieure ou égale à deux Angstroms. L'utilisation de la médiane est préférable que la moyenne, car moins affectée par les valeurs extrêmes [9].
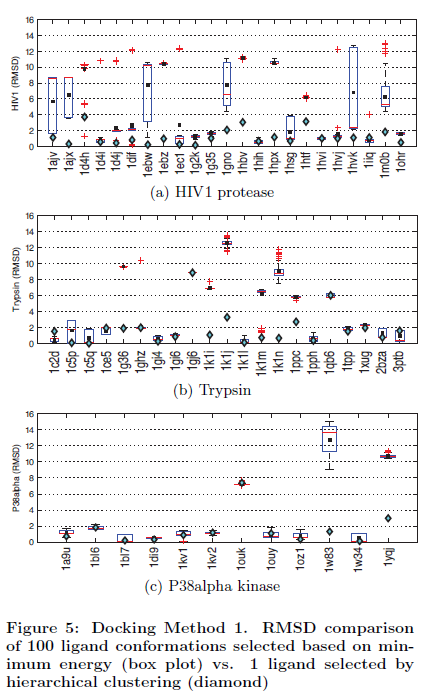
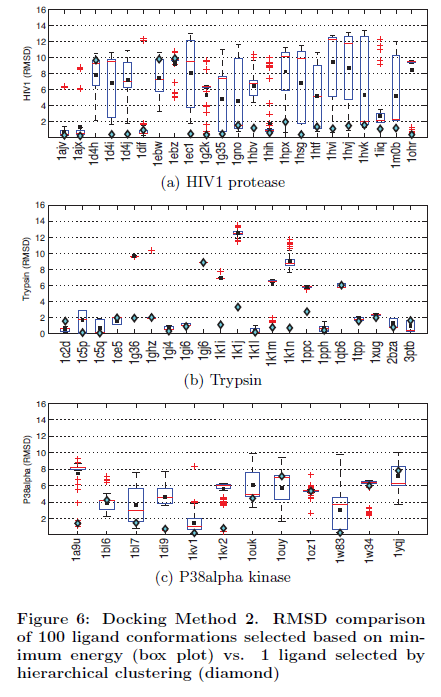
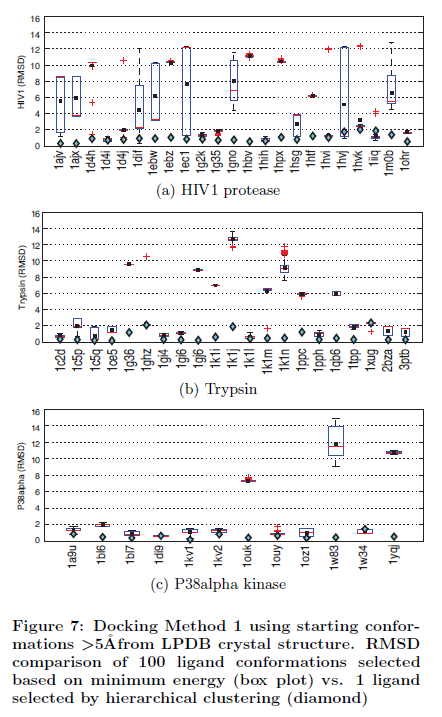
Les figures 5.a, b et c présentent les deux comparaisons de validation pour l’intérêt des trois protéines pour la méthode 1. Les figures 6.a, b et c présente les deux comparaisons pour les mêmes trois protéines avec la méthode 2, et les figures 7.a, b et c présentent les comparaisons pour les trois mêmes protéines avec la méthode 1 avec une conformation définie par l'utilisateur qui a été de moins de 5 Angstroms d’espacement de la structure cristalline. Les figures 5.a, 6.a et 7.a se rapportent à la protéase du VIH1, les figures 5.b, 6.b et 7.b se référent à la trypsine, et les figures 5.c, 6.c et 7.c se rapportent à P38alpha kinase. Sur l’axe des abscisses, nous montrons les différents complexes et sur l’axe des ordonnées, nous montrons leur RMSD, le plus faible étant le meilleur. Les losanges représentent les RMSD du groupe candidat WRT de la structure cristalline. Les graphiques représentent la boîte du RMSD des 100 conformations choisis en fonction de l'énergie.
La boîte de données graphiques se compose de sept différents éléments d'information. Les favoris du bas s’étendent du 10e pourcentage (décile inférieur) au 90e pourcentage supérieur (décile supérieur). Les valeurs aberrantes sont placées à la fin des déciles supérieurs favoris. Le haut, le bas, et le trait au milieu de la boîte correspond au 75e pourcentage (en haut), 25e pourcentage (en bas), et 50e pourcentage (au milieu). Un carré indique la moyenne arithmétique.
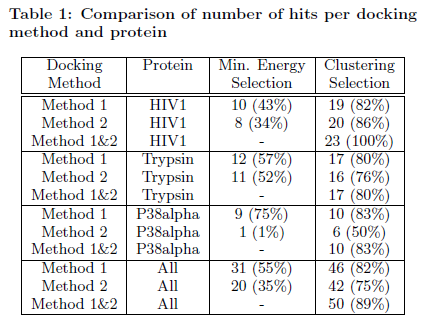
Pour la méthode 1 avec la protéase du VIH1, l'approche énergétique est capable d'identifier seulement 10 des 23 conformations quasi-native (soit un taux de succès de 43%) tandis que notre méthode de clustering capte 19 des 23 conformations quasi-native (soit un taux de succès de 82%). Pour la trypsine, l'approche énergétique identifie seulement 12 des 21 conformations quasi-native (taux de succès de 57%) et notre méthode de clustering capte 17 des 21 conformations quasi-native (taux de succès de 80%). Pour la kinase P38alpha, l'approche énergétique identifie 9 des 12 conformations quasi-native (taux de succès de 75%) et notre méthode de clustering remporte 10 des 12 conformations quasi-native (taux de succès de 83%). Lorsque nous considérons la méthode 2, la plus intensive en calculs, pour la protéase du VIH, l'approche énergétique est capable d'identifier seulement 8 des 23 conformations quasi-native (taux de succès de 34%) alors que notre méthode de clustering capte 20 des 23 quasi-native conformations (taux de succès de 86%). Pour la trypsine, l'approche énergétique identifie seulement 11 des 21 conformations quasi-native (taux de succès de 52%) et notre méthode de classification représente 16 des 21 conformations quasi-native (taux de succès de 76%). Pour la kinase P38alpha l'approche énergétique identifie 1 des 12 conformations quasi-native (taux de réussite de 0,8%) et notre approche prend en compte 6 des 12 conformations quasi-native (taux de succès de 50%). Le tableau 1 récapitule les taux de succès pour les deux méthodes d'amarrage. Comme le montre le tableau, dans le cadre de l’étude, notre approche surpasse l'approche énergétique pour tous les complexes et pour chaque méthode. Grâce à notre méthode de classification, nous pouvons voir qu'aucune des deux méthodes d'accueil sont nettement supérieures à l'autre. La combinaison des deux méthodes d'amarrage (méthode 1 et 2) permet de renforcer encore la précision de nos prédictions pour la protéase du VIH pour lesquels nous avons observé un taux de succès de 100%. Pour les deux autres protéines, nous avons observé le même taux de succès. Dans le tableau, nous ne comparons pas la sélection de l'énergie en fonction basée en combinant les deux méthodes d'accueil, car elles sont composées d'approximations tout à fait différentes de l'énergie potentielle.
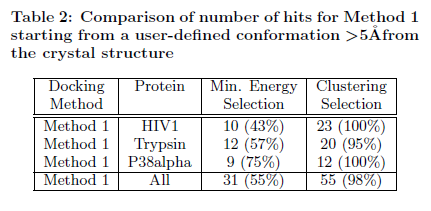
Le tableau 2 résume les taux de succès pour la Méthode d’accueil 1 lorsque le processus d'accueil commence à partir d'une conformation définie par l'utilisateur à partir d'au moins 5 Angströms à partir de la conformation de la structure cristalline BDPT. Pour la protéase du VIH1, l'approche énergétique est en mesure d'identifier que 10 des 23 conformations quasi-native (taux de succès de 43%) tandis que notre méthode de classification englobe les 23 conformations quasi-native (taux de succès de 100%). Pour la protéine trypsine, l'approche énergétique est en mesure d'identifier que 12 des 21 conformations quasi-native (taux de succès de 57%) tandis que notre méthode de clustering capte 20 des 21 conformations quasi-native (taux de succès de 95%). Pour la kinase P38alpha, l'approche énergétique identifie 9 des 12 conformations quasi-native (taux de succès de 75%) et notre approche prend en compte 12 des 12 conformations quasi-native (taux de succès de 100%). Lorsque l'on considère les trois ensembles de complexes avec l'approche énergétique nous avons un taux de succès de seulement 55% alors que notre méthode de regroupement identifiés à proximité de la conformation native-ligand est bonne dans 98% des cas. Comme le montre le tableau 2, notre cadre surpasse toujours l'approche basée sur l'énergie pour les deux ensembles de complexes et montre des tendances similaires comme pour la méthode 1 quand nous utilisons des conformations de ligand de départ aléatoires qui sont générées par MD à partir de la conformation ligand cristallographique. En outre, les données du tableau 2 montrent que les conclusions finales de cette étude sont robustes et non influencées par le fait de commencer la recherche de conformation par la conformation quasi-native du ligand initial.
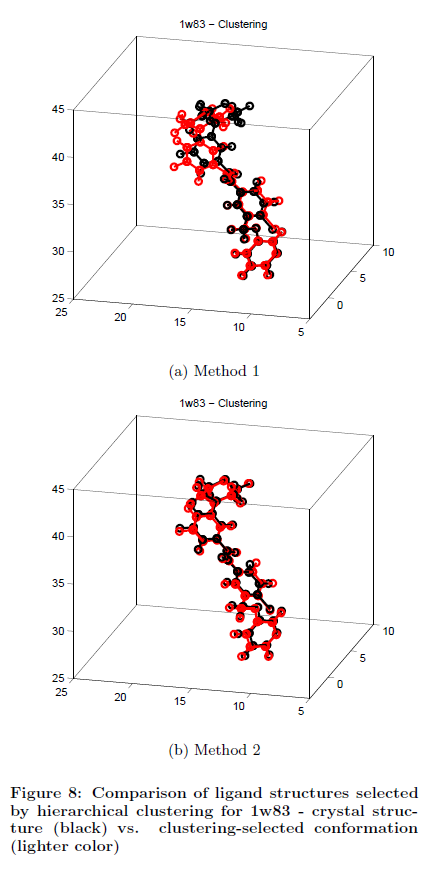
Si l'on reprend le même complexe (1w83) présenté dans la figure 3, et que nous utilisons cette fois notre méthode de classification pour la sélection de la conformation candidate, nous constatons que nous sommes en mesure de trouver une conformation quasi-native pour les deux méthodes d'amarrage (Figure 8.a pour la méthode 1 et la figure 8.b pour la méthode 2). Le ligand noir, représentant le ligand dans la structure cristalline BDPT, chevauche pratiquement le ligand gris, qui représente dans ce cas la conformation ligand candidate sélectionnés par notre classification hiérarchique probabiliste. Contrairement à la sélection ligand fondées sur l'énergie, notre regroupement probabiliste est capable d'identifier avec précision la conformation ligand quasi native indépendamment de la méthode d'accostage.
Pour mieux illustrer le comportement de notre méthode de clustering et de sa capacité à identifier un nombre variable de clusters dynamique, la figure 9 montre le résultat pour neuf des complexes en utilisant la méthode 2 (trois pour le VIH,, 1d4i, 1dif, et 1ebw; trois pour la trypsine, -1k1m, 1c2d, et 3ptb, et trois pour P38alpha,, 1a9u, 1oz1, et 1ouy). Pour chaque protéine, nous présentons un complexe pour laquelle notre méthode surpasse clairement l'approche naïve (colonne de gauche), un complexe pour laquelle notre méthode a une précision similaire à l'approche naïve (colonne centrale), et un complexe pour lequel l'approche naïve a une meilleure précision (colonne de droite). Nous utilisons la méthode 2, puisque la méthode 1 est toujours dans notre cadre soit supérieur ou égal à la précision de l'approche naïve (voir Figure 5). Ce n'est pas toujours le cas pour la méthode 2 (voir Figure 6). Après le regroupement terminé, nous avons la cartographions chaque conformation de chaque groupe par rapport à son énergie (abscisse) et ses RMSD par rapport à la structure cristalline (ordonnée). Les différentes couleurs indiquent les différents groupes (comme l'indique la légende). Le groupe le plus profond (zone de gris) dans la hiérarchie est le groupe cible contenant le candidat montré comme une ligne solide horizontale. La meilleure conformation choisis en fonction de son énergie minimale est indiquée par une ligne horizontale en pointillés. Comme le montre la figure 9, la profondeur du cluster hiérarchique (nombre de grappes) est variable, allant de deux pour, par exemple, 1dif, à quatre, par exemple pour, 1d4i, et dépend du paysage énergétique du complexe [6]. Le nombre maximal de clusters dans l’ensemble de données D @ H est de six. Aucune intervention humaine n'est nécessaire pour définir la profondeur de clustering.

En raison de son taux de réussite élevé, le cadre proposé peut être utilisée sans être changé pour sélectionner des conformations de ligand quasi-native dans les simulations d'amarrage protéine-ligand lorsque les structures cristallines sont inconnus. En outre, le cadre peut être utilisé pour la sélection de conformations quasi-native dans d'autres simulations pertinentes, telles que le repliement des protéines et la prédiction des protéines.

6- Travaux connexes
Des travaux antérieurs ont utilisé avec succès différentes techniques pour explorer l'espace de recherche des conformations d'accueil. Une approche commune non basée sur le regroupement est la simulation d'échantillonnage par raffinement. L'approche par raffinement trouve a quel temps d'exécution les conformations vont probablement être quasi-native et exécute ensuite un vaste échantillonnage autour des conformations prévues. D’importants travaux vont dans cette direction : Yang [16] et Liang [13].
Yang [16] sous-estime un jeu de minimums d'énergie locaux et utilise ce modèle pour conduire plus loin l'échantillonnage. L’algorithme de Yang explore la surface d'énergie libre étendue par les complexes et les prédictions d’accueil trouvées avec une exactitude de 5°A. de la structure en cristal. Liang [13] proposent une méthode pour affiner la précision de la valeur de la confirmation d’accueil protéine-ligand prédite qui repose sur plusieurs fonctions d’évaluation et un algorithme de calcul efficace pour le raffinement de conformation. En utilisant cette méthode, les auteurs ont pu améliorer la précision des conformations prédites de 0,5 ° A comparé à d'autres méthodes. Les méthodes publiées dans [16] et [13] améliore la précision des méthodes d'accueil et augmente la probabilité de sélection de conformations quasi-native, mais elles ne fournissent pas de sélection automatique de conformation quasi-native.
Des méthodes de classification ont également été utilisées pour trouver un éventuel ensemble de conformations quasi-native d'accueil réduit. Ce groupe de conformations est analysé manuellement par des experts qui décident quelles conformations sont de bons candidats et celles qui ne le sont pas. A notre connaissance, aucune de ces méthodes de classification sont entièrement automatiques et nécessitent un certain degré d'intervention humaine. Les approches de classement comprennent les travaux de Lorenzen [14], Bouvier [3], et Chang [6].
Lorenzen [14], sélectionne les conformations d’accueil quasi-native reposant sur une démarche de clustering considérant qu'un plus grand cluster est plus susceptible d'avoir des meilleurs candidats de conformations. Comme dans notre travail, la sélection basée sur la taille du cluster surpasse le classement basé sur la valeur de l'énergie. Le clustering est entraînée par des seuils définis manuellement et peut trouver des conformations d'accueil avec une précision d'environ 5 ° A. Bouvier [3] utilise une carte de Kohonen auto-organisation (SOM) qui est formée dans une phase préliminaire utilisant des descripteurs de contact médicament-protéine. Comme dans le présent document, les travaux de Bouvier décrivent la possibilité de surmonter les problèmes inhérents aux fonctions d’évaluation en utilisant une analyse statistique de différentes propriétés des conformations amarrées. Chang [6] a effectué une analyse typologique simple des simulations d'accueil et utilise la taille des grappes pour estimer l'entropie de vibration des conformations résultant. La fréquence de conformation fournit des informations sur le paysage énergétique de la liaison. Une haute fréquence est une mesure de l'entropie favorable dans le processus de liaison.
Les méthodes basées sur le regroupement présentées ci-dessus utilisent des algorithmes de clustering pour grouper les conformations d'accueil et ne sont pas entièrement automatiques. Lorsqu'elle est fondée sur des seuils, comme dans le cas [14, 6], les méthodes exigent des réglages supplémentaire pour avoir des décisions optimales; des paramètres de réglage différents produisent des résultats différents selon le jeu de complexes.. Lorsqu'elles sont fondées sur des ensembles de données de formation, comme dans le cas de [3], les méthodes exigent une validation plus étendue pour prouver leur robustesse. Cette validation étendue est manquante dans [3]. En revanche, notre cadre ne nécessite pas de réglage des paramètres et peut être appliqué sans modification à une nouvelle série de complexes inédits.

7- Conclusion
Les technologies distribuées de pointe, tels que le cloud computing et le calcul bénévole, permettent de fournir aux scientifiques un moyen efficace et évolutif pour effectuer des simulations de calcul d’accueil coûteux à un rythme jamais vu auparavant. Dans cet article nous utilisons Docking @ Home, un projet de calcul bénévole, pour exécuter ce type de simulations. Plus précisément, D @ H utilise 30.000 ordinateurs volontaires pour simuler le comportement de petites molécules (appelées ligands) lors de l'ancrage à une protéine pour contrôler ses fonctions.
Soutenu par les capacités de D H @ nous avons cherché dans le grand espace des conformations protéine-ligand d'accueil pour trois protéines majeures et 56 ligands. Lorsque nous utilisons les méthodes basées uniquement sur l'énergie, dans 35% (pire scénario) et 55% (meilleur scénario) des cas nous avons pu identifier une conformation ligand quasi-native. Nous avons considérablement amélioré cette précision de pointage à l'aide de notre nouvelle méthode qui permet une analyse automatique des résultats d'amarrage protéine-ligand, même en présence de l'incertitude des données. Notre méthode est basée sur une classification probabiliste hiérarchique qui organise efficacement les données dans un nombre variable d'ensembles en fonction de leur géométrie. Chaque jeu a une solution unique ainsi, les conclusions scientifiques peuvent être atteintes dans un délai court, en analysant seulement un nombre réduit de solutions. En utilisant notre procédé et un ligand généré de façon aléatoire comme notre conformation de départ, nous avons pu identifier les conformations ligands quasi-native dans 75% (pire) et 89% (meilleur scénario) des cas. En commençant d'une conformation impartiale comme un ligand dont la conformation est > 5°A de la structure correcte de cristal, notre méthode surpasse toujours la sélection à base d'énergie : nous avons identifié des conformations ligand quasi-native dans 98% des cas pour les trois protéines considérée, alors que la méthode basée sur l'énergie trouve une telle conformation que dans 55% des cas pour le même ensemble de données.

Remerciements
Ce travail a été financé par la NSF, subvention # 0941318: «CDI Type 1: Combler le fossé entre la prochaine génération d’ordinateurs haute performance hybride basé sur la physique et les modèles de calcul pour la description quantitative de reconnaissance moléculaire», et subvention # 0922657 'MRI: Acquisition d'une installation pour les approches de calcul des problèmes à l'échelle moléculaire», et par l'armée américaine, subvention ARO 54723-CS" L’aide des ordinateurs pour la modélisation de médicaments sur les nouveaux ordinateurs hybrides à haut rendement, et par la bourse # 171595 CONACyT. Les auteurs tiennent à remercier Charles L. Brooks III pour ses précieux conseils et les volontaires de Docking @ Home pour nous fournir des ressources essentielles.
Références
[1] D. P. Anderson. Boinc: A system for public-resource
computing and storage. In Proceedings of the 5th
IEEE/ACM International Workshop on Grid Computing.,
pages 4–10, November 2004.
[2] K. Bckbro, S. Lwgren, K. Osterlund, J. Atepo, T. Unge,
J. Hultn, N.M. Bonham, W. Schaal, A. Karln, and
A. Hallberg. Unexpected binding mode of a cyclic
sulfamide hiv-1 protease inhibitor. Journal of Medical
Chemistry, 40:898–902, 1997.
[3] G. Bouvier, N. Evrard-Todeschi, J. P. Girault, and
G. Bertho. Automatic clustering of docking poses in virtual
screening process using self-organising map. Bioinformatics
Advance Access, 2009.
[4] R. L. Cannon, J. V. Dave, and J. C. Bezdek. Efficient
implementation of the fuzzy c-means clustering algorithms.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 8:248–255, 1986.
[5] S. Ceri and R. Manthey. Chimera: A model and language
for active dood systems. In In Proceedings of the 2nd
East-West Database Workshop, Workshops in Computing,
pages 3–16. Springer, 1994.
[6] M. W. Chang, R. K. Belew, K. S. Carroll, A. J. Olson, and
D. S. Goodsell. Empirical entropic contributions in
computational docking: Evaluation in aps reductase
complexes. Journal of Computational Chemistry,
29:1753–1761, 2008.
[7] F. Dullweber, M.T. Stubbs, D. Musil, J. Strzebecher, and
G. Klebe. Factorising ligand affinity: a combined
thermodynamic and crystallographic study of trypsin and
thrombin inhibition. Journal of Molecular Biology,
313:593–614, 2001.
[8] M. Feig, A. Onufriev, M. S. Lee, W. Im, D. A. Case, and
C. L. Brooks III. Performance comparison of generalized
born and poisson methods in the calculation of electrostatic
solvation energies for protein structures. Journal of
Computational Chemistry, 25:265–84, 2004.
[9] P. C. D. Hawkins, G. L. Warren, A. G. Skillman, and
A. Nicholls. How to do an evaluation: pitfalls and traps. J.
of Computer Aided Molecular Design, 22:179–190, 2008.
[10] W. Humphrey, A. Dalke, and K. Schulten. VMD – Visual
Molecular Dynamics. Journal of Molecular Graphics,
14:33–38, 1996.
[11] A. N. Jain. Bias, reporting, and sharing: computational
evaluations of docking methods. Journal of Computer
Aided Molecular Design, 22:201–212, 2008.
[12] M. S. Lee, M. Feig, F. R. Salsbury Jr., and C. L. Brooks
III. New analytic approximation to the standard molecular
volume definition and its application to generalized born
calculations. Journal of Computational Chemistry,
24:1348–56, 2003.
[13] S. Liang, G. Wang, and Y. Zhou. Refining near-native
protein-protein docking decoys by local resampling and
energy minimization. PROTEINS: Structure, Function,
and Bioinformatics, pages 309–316, 2008.
[14] S. Lorenzen and Y. Zhang. Identification of near-native
structures by clustering protein docking conformations.
PROTEINS: Structure, Function, and Bioinformatics,
68:187–194, 2007.
[15] LPDB - protein-ligand database. http://lpdb.scripps.edu/.
[16] Y. Shen, I. C. Paschalidis, P. Vakili, and S. Vajda. Protein
docking by the underestimation of free energy funnels in
the space of encounter complexes. PLOS Computational
Biology, 4, 2008.
[17] W. S. Student Gosset. The probable error of a mean.
Biometrika, 6:1–25, 1908.
[18] Z. Wang, B.J. Canagarajah, J.C. Boehm, S. Kassis, M.H
Cobb, P.R Young, S. Abdel-Meguid, J.L Adams, and E.J.
Goldsmith. Structural basis of inhibitor selectivity in map
kinases. Structure, 6:1117–28, 1998.
[19] B. L. Welch. The generalization of ’student’s’ problem.
Biometrika, 34:28–35, 1947.
Traduction
Alliance Francophone
(Ryzen, Ousermaatre, Bcoz)


