4- Un algorithme de regroupement probabiliste et hiérarchique
Les résultats de la section 3 soulèvent une question importante. Compte tenu de l'inexactitude des algorithmes d'accueil et des millions de conformations recueillis, comment les scientifiques peuvent-ils choisir ceux qui sont plus susceptibles de se produire dans la nature, étant donné que l'énergie n'est pas toujours une mesure d’évaluation fiable?
Les algorithmes de classification peuvent être utilisés pour affiner les données avec succès dans les phases de post-traitement. Ils peuvent également être utilisés pour identifier les résultats qui sont représentatifs des solutions dans les simulations. Les algorithmes de regroupement peuvent être partitionnels ou hiérarchiques. Un regroupement partitionnel divise les données selon une mesure de distance. Une limite importante de cette famille d'algorithmes, est que lorsqu'il est utilisé avec des données telles que les conformations protéine-ligand recueillies dans D @ H, le nombre de clusters doit être connue a priori. Dans D @ H, ce nombre n'est pas connu et une estimation précise et efficace de ce nombre n'est pas possible ni quand la simulation est en cours, ni quand la simulation est terminée et que tous les résultats sont collectés. D'autre part, les algorithmes de classification hiérarchique n'ont pas besoin de connaissances préalables sur le nombre final de clusters et peuvent être classés en agglomération ou en division. Un cluster hiérarchique ascendant commence avec chaque élément comme un groupe particulier, puis fusionne des éléments similaires dans de grosses grappes. Un algorithme hiérarchique de division commence avec un seul groupe comprenant toutes les données et les répartit ensuite en fonction d'une certaine distance métrique. Le défi pour la classification hiérarchique consiste à déterminer la meilleure profondeur de regroupement, c'est à dire, savoir quand arrêter la fusion ou la division des clusters. Une autre condition importante pour l'utilisation de toute méthode de classification est la capacité d'organiser automatiquement les données sans avoir toutes les données déjà classées, étiquetées, ou annotées et sans intervention humaine.
De toute évidence, aucune des techniques de clustering ci-dessus ne propose un champ d'application de manière efficace et précis de regroupement des ensembles de données tels que les résultats de D @ H, quand ils sont pris individuellement. Par conséquent, plutôt que d'utiliser une technique de clustering unique, nous proposons de combiner deux techniques pour tirer parti de leurs points forts. En particulier, nous proposons d'utiliser un cadre probabiliste hiérarchique qui combine (1) la capacité de faire face à l'incertitude des données en utilisant un fuzzy (clustering avec partitionnement) (2) la capacité d'identifier le nombre de grappes nécessaires à l'exécution en utilisant un algorithme de division hiérarchique pour lequel la hiérarchie cluster-profondeur est déterminée de manière probabiliste basée sur la variabilité du résultat. Plutôt que d'utiliser les énergies, nous utilisons les conformations géométriques des ligands comme entrée à notre regroupement et le RMSD entre les résultats des ligands D @ H et la distance métrique. Notez qu'ici nous nous référons à la RMSD comme mesure pour comparer les résultats de ligands entre eux et nous ne nous référons pas à la structure cristalline qui est inconnu pour nous pendant le processus d’évaluation. Nous supposons également que D @ H nous donne le nombre suffisant d'échantillons, et ainsi s’approcher vers des solutions de simulations quasi-native. Notre structure hiérarchique probabiliste est en mesure d'effectuer un regroupement efficace sans surveillance des grands ensembles de données de D @ H, même en présence d'incertitude.
Pour être plus précis, le Partitionnement Moyen Flou (Fuzzy C-Means (FCM)) [4] permet un partitionnement non disjoint des données, permettant de traiter les incertitudes. Dans un partitionnement traditionnel, chaque élément appartient à un seul groupe de données ; au contraire, dans un partitionnement flou chaque élément a un score, ou degré d’appartenance à chacun des groupes de données. Les éléments appartiennent à chaque groupe avec un degré différent dépendant de leur distance au centre (appelé également centroïde) de ce groupe.
Plus formellement, pour chaque ensemble de données D et chaque élément di appartenant à D, on détermine un vecteur score si donnant la probabilité que di soit un élément de chaque partitionnement : si = si ,1,si ,2,…si ,k où k est le nombre prédéfini de partitions et où la somme des si vaut 1. FCM est un algorithme récursif : on commence par sélectionner k éléments au hasard (appelé centroïdes initiaux) dans le jeu de données D. La seconde étape est de calculer le vecteur score si pour chaque élément di, où le degré d’appartenance est l’inverse normalisé de la distance au centroïde Ck (voir équation 1), la distance(x,y) étant une fonction personnalisée qui peut être ajustée selon le type de données traitées. Pour chaque groupe, un nouveau centroïde C’k est calculé comme étant la moyenne de tous les points pondérés par leur degré d’appartenance au groupe (voir équation 2). Ce procédé est réitéré jusqu’à la stabilisation des centroïdes, c'est-à-dire jusqu’à ce qu’ils restent inchangés.
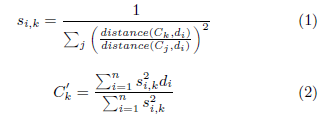
Dans notre architecture, FCM travaille de concert avec un algorithme de partitionnement hiérarchique des données. Cet algorithme commence avec un jeu de données Dm (m≠0) et utilise FCM pour le diviser en deux sous-ensembles (k=2), l’un étant défini comme le complément de l’autre (Dm+1 et D-Dm+1). Les éléments redondants (ceux n’appartenant pas fortement à un sous-ensemble ou l’autre) étant éliminés temporairement de ces deux partitions. Notre algorithme hiérarchique probabiliste sélectionne la partition (Dm+1) avec une probabilité proportionnelle à sa taille et inversement proportionnelle à sa variance interne. Cette partition est ensuite utilisée pour les partitionnements suivants. Le processus continue jusqu’à ce que la moyenne des deux partitions (Dm+1 et D- Dm+1) soit égale avec une significativité statistique de 0.05. Pour déterminer si les moyennes des groupes sont égales, nous utilisons le t-test de Welch [19] tel que montré dans l’équation 3, où Cm+1 est le centroïde de Dm+1, Cm’+1 est le centroïde de Dm- Dm+1, et σm+1 et σm’+1 sont leurs déviation standard respectives. Une fois le t-test calculé, nous trouvons sa p-value d’après une t-distribution de Student [17]. On sauvegarde les centroïdes et continue la partition jusqu’à ce que la p-value soit inférieure à 0.05 et que le nombre d’éléments de Dm+1 reste plus grand qu’un seuil défini par la précision souhaitée (par exemple 1 Angström). A chaque étape, la hiérarchie des centroïdes est conservée et utilisée comme résumé de l’espace des données.
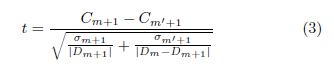
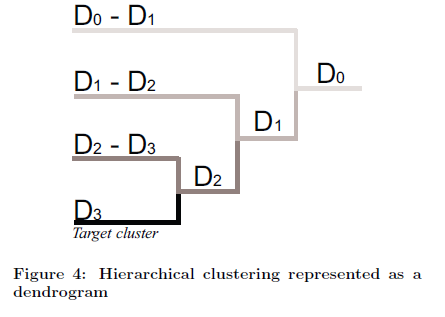
Notre architecture de partitionnement probabiliste hiérarchique peut être utilisées pour (1) organiser automatiquement des données en jeux disjoints (2) trouver une solution globale, probablement unique, à partir de résultats multiples indépendants. La figure 4 présente un exemple pour lequel l’algorithme hiérarchique est représenté graphiquement comme une structure arborescente (dendrogramme). Pour cette figure particulière, les centroïdes pour D0, D0-D1, D1, D1-D2, D2, D2-D3, et D3 sont déterminés et peuvent être utilisés pour résumer et analyser les différentes dimensions du jeu de données. Par définition, le dernier groupe est également le plus compact (c'est-à-dire le plus grand avec la plus petite variance interne). En conséquence, le centroïde D3 peut être utilisé comme solution la plus probable de l’ensemble de données.